
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,m<2或m>6,即可得出结论.
解答 解:方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,
∴m<2或m>6,
∴“2<m<6”是“方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程”的既不充分也不必要条件,
故选D.
点评 本题考查充要条件的判断,考查学生的计算能力,利用方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1为双曲线的方程,则(m-2)(6-m)<0,求出m的范围是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-2,2] | C. | [-1,3] | D. | [0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${e^{cos{θ_1}}}-{e^{cos{θ_2}}}>lncos{θ_1}-lncos{θ_2}$ | |
| B. | ${e^{cos{θ_1}}}-{e^{cos{θ_2}}}<lncos{θ_1}-lncos{θ_2}$ | |
| C. | $cos{θ_2}{e^{cos{θ_1}}}>cos{θ_1}{e^{cos{θ_2}}}$ | |
| D. | $cos{θ_2}{e^{cos{θ_1}}}<cos{θ_1}{e^{cos{θ_2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
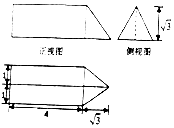
| A. | $4\sqrt{3}+1$ | B. | $4\sqrt{3}$ | C. | $24+2\sqrt{3}+\sqrt{15}$ | D. | $24+3\sqrt{3}+\sqrt{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.| 分组 | 频数 |
| [2,4) | 2 |
| [4,6) | 10 |
| [6,8) | 16 |
| [8,10) | 8 |
| [10,12] | 4 |
| 合计 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com