
分析 (1)以AB边所在直线为x轴,以AB边的垂直平分线为y轴建立平面直角坐标系,利用AC与BC边所在直线的斜率之积为定值m,建立方程,即可求动点C的轨迹方程;
(2)分类讨论,联立方程组,即可求P、Q两点的中点M的轨迹方程.
解答 解:以AB边所在直线为x轴,以AB边的垂直平分线为y轴建立平面直角坐标系
则A(-4,0),B(4,0)
(1)设点C的坐标为(x,y),则${k_{AC}}=\frac{y}{x+4},{k_{BC}}=\frac{y}{x-4}$,
∴${k_{BC}}{k_{AC}}=\frac{y}{x-4}•\frac{y}{x+4}=\frac{y^2}{{{x^2}-16}}=m$,
即mx2-y2=16m----------------------------------------------------------------------------------(2分)
当m=0时,动点C的轨迹方程为y=0(x≠±4),
表示x轴所在直线去掉A、B两点剩下的部分--------------------------------------------(3分)
当m>0时,动点C的轨迹方程为$\frac{x^2}{16}-\frac{y^2}{16m}=1(x≠±4)$
表示焦点在x轴上的双曲线去掉A、B两点剩下的部-----------------------------------(4分)
当-1<m<0时,动点C的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{-16m}=1(x≠±4)$
表示焦点在x轴上的椭圆去掉A、B两点剩下的部分-----------------------------------(5分)
当m<-1时,动点C的轨迹方程为 $\frac{y^2}{-16m}+\frac{x^2}{16}=1(x≠±4)$
表示焦点在y轴上的椭圆去掉A、B两点剩下的部分------------------------------------(6分)
当m=-1时,动点C的轨迹方程为 x2+y2=16(x≠±4)
表示以AB为直径的圆去掉A、B两点剩下的部分---------------------------------------(7分)
(2)当m=1时,动点C的轨迹方程为$\frac{x^2}{16}-\frac{y^2}{16}=1(x≠±4)$,--------------------(8分)
当直线l的斜率不存在时,显然不可能与$\frac{x^2}{16}-\frac{y^2}{16}=1(x≠±4)$有交点,舍去;
当直线l的斜率存在时,设l的方程为y=kx+1,设P(x1,y1),Q(x2,y2),M(x0,y0)
联立方程组$\left\{\begin{array}{l}\frac{x^2}{16}-\frac{y^2}{16}=1(x≠±4)\\ y=kx+1\end{array}\right.$,
消去y得:(1-k2)x2-2kx-17=0
由题意得:x1、x2是此方程的解
所以${x_1}+{x_2}=\frac{2k}{{1-{k^2}}}$∴${y_1}+{y_2}=(k{x_1}+1)+(k{x_2}+1)=\frac{2}{{1-{k^2}}}$
所以$\left\{\begin{array}{l}{x_0}=\frac{{{x_1}+{x_2}}}{2}=\frac{k}{{1-{k^2}}}\\{y_0}=\frac{{{y_1}+{y_2}}}{2}=\frac{1}{{1-{k^2}}}\end{array}\right.$$\frac{x_0}{y_0}=k$,所以得$y_0^2-x_0^2-{y_0}=0$----------------------------(10分)
又直线l与动点C的轨迹方程有两个不同的焦点,
则$\left\{\begin{array}{l}△={(-2k)^2}+4×17(1-{k^2})>0\\ 1-{k^2}≠0\\{k^2}≠\frac{1}{16}\end{array}\right.$∴${k^2}<\frac{17}{16}$且${k^2}≠\frac{1}{16}$且k2≠1,∴${y_0}≥1且{y_0}≠\frac{16}{15}$或y0<-16
所以P、Q两点的中点M的轨迹方程为${y^2}-{x^2}-y=0(y≥1且{y_{\;}}≠\frac{16}{15}$或y<-16)-----------------------(12分)
点评 本题考查轨迹方程,考查直线与双曲线位置关系的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+2 | C. | 1+2+22 | D. | 1+2+22+23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2020,-2017) | B. | (-∞,-2017) | C. | (-2018,-2017) | D. | (-∞,-2020) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
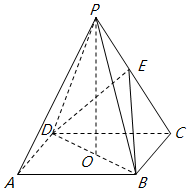 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 0.9 | 1.9 | 3.2 | 4.4 |
| A. | 1.5 | B. | 1.2 | C. | 0.9 | D. | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com