
| A. | 4 | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $\sqrt{7}$ |
分析 根据平面向量的数量积,计算模长$|{3\overrightarrow a+\overrightarrow b}|$即可.
解答 解:$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,
∴$\overrightarrow{a}$$•\overrightarrow{b}$=1×1×cos60°=$\frac{1}{2}$,
∴${(3\overrightarrow{a}+\overrightarrow{b})}^{2}$=9${\overrightarrow{a}}^{2}$+6$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=9+6×$\frac{1}{2}$+1=13,
∴$|{3\overrightarrow a+\overrightarrow b}|$=$\sqrt{13}$.
故选:B.
点评 本题考查了利用平面向量的数量积求模长的应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{13}$ | C. | $\sqrt{21}$ | D. | $\sqrt{57}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α⊥β,α∩β=l,m⊥l | B. | α∩γ=m,α⊥γ,β⊥γ | C. | α⊥γ,β⊥γ,m⊥α | D. | n⊥α,n⊥β,m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
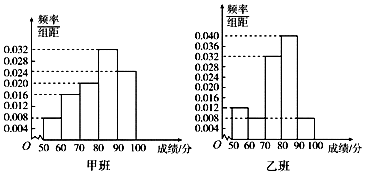
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的最小正周期为$\frac{π}{4}$ | B. | 函数是偶函数 | ||
| C. | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D. | 函数在$[{\frac{2π}{3},\frac{5π}{6}}]$上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{3})$ | B. | (1,2] | C. | $(\sqrt{3},+∞)$ | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com