
如图,直线y=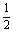 x严与抛物线y=
x严与抛物线y=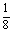 x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.
x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.
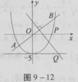
(1)求点Q的坐标
(2)当P为抛物线上位于线段AB下方(含点A、B)的动点时,求△OPQ面积的最大值.
(1)解法一:直线l过点M(0,1),设其斜率为A,则J的方程为y=kx+1.
记A(x1,y1)、B(x2,y2),由题设可得A、B的坐标(x1,y1)、(x2,y2)是方程组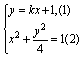 的解.
的解.
将①代入②并化简得.(4+k2)x2+2kx-3=0.所以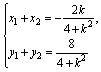 于是
于是
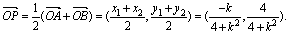
 设点P的坐标为(x,y),则
设点P的坐标为(x,y),则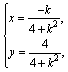
消去参数k得
4x2+y2-y=0. ③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方程为
4x2+y2-y=0
解法二:设点P的坐标为(x,y),因A(x1,y1)、B(x2,y2)在椭圆上,所以
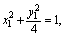 ④
④
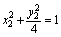 ⑤
⑤
④-⑤得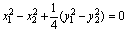
所以(x1-x2)(x1+x2)+ (y1-y2)(y1+y2)=0
(y1-y2)(y1+y2)=0
当x1≠x2时,有
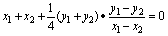 ⑥
⑥
并且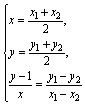 ⑦
⑦
将⑦代入⑥并整理得4x2+y2-y=0.⑧
当x1=x2时,点A、B的坐标为(0,2)、(0,-2),这时点p的坐标为(0,0)也满足⑧,所以点P的轨迹方程为
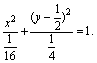
(Ⅱ)解法:由点P的轨迹方程知x2≤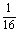 。 即-
。 即- ≤x≤
≤x≤ 所以
所以
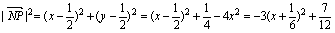
故当x= 时,
时,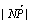 取得最小值,最小值为
取得最小值,最小值为 ,当x=
,当x=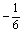 时,
时,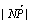 取得最大值,最大值为
取得最大值,最大值为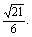


科目:高中数学 来源: 题型:
设函数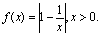
(Ⅰ)证明:当0<a<b,且f(a)=f(b)时,ab>1;
(Ⅱ)点P(xo,yo)(0<xo<1)在曲线y=f(x)上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用xo表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点
(1)设l的斜率为1,求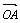 与
与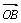 夹角的大小;
夹角的大小;
(Ⅱ)设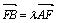 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆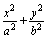 =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足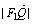 =2a,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a,点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足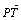 ·
·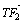 =0,|
=0,|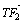 |≠0.
|≠0.
(1)设x为点P的横坐标,证明|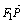 |=a+
|=a+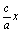 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2,若存在,求∠F1MF2的正切值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设F为抛物线y2=2px(p>0)的焦点,A,B,C为该抛物线上三点,当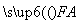 +
+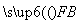 +
+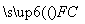 =0,且|
=0,且|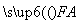 |+|
|+|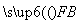 |+|
|+|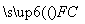 |=3时,此抛物线的方程为( )
|=3时,此抛物线的方程为( )
A.y2=2x B.y2=4x
C.y2=6x D.y2=8x
查看答案和解析>>
科目:高中数学 来源: 题型:
设i是虚数单位,复数z和w满足zw+2iz-2iw+1=0
(1)若z和w又满足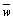 -z=2i,求z和w值。
-z=2i,求z和w值。
(2)求证:如果|z|=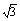 ,那么|w-4i|的值是一
,那么|w-4i|的值是一 个常数,并求这个常数。
个常数,并求这个常数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com