Question

7．已知：在四棱锥P-ABCD中，PD⊥平面ABCD，PD=CD=BC=2AD，AD∥BC，∠BCD=90°
（Ⅰ）求证：BC⊥PC；
（Ⅱ）求直线PA与平面PBC所成的正弦值．

Answer 1

分析 （Ⅰ）首先根据已知条件利用线面垂直转化成线线垂直，进一步利用线面垂直的判定定理得到线面垂直，最后转化成线线垂直．
（Ⅱ）首先利用直线间的两两垂直，建立空间直角坐标系，利用法向量求出线面之间的夹角．

解答 证明：（Ⅰ）在四棱锥P-ABCD中，PD⊥平面ABCD，
所以：PD⊥BC，
又∠BCD=90°，
所以：BC⊥CD，
则：BC⊥平面PCD，
则：BC⊥PC．
（Ⅱ）由于在四棱锥P-ABCD中，PD⊥平面ABCD，AD∥BC，∠BCD=90°，
所以：∠ADC=90°．
建立空间直角坐标系D-xyz，PD=CD=BC=2AD，设AD=1，直线PA与平面PBC所成的角为θ，
则：A（1，0，0），P（0，0，2），C（0，2，0），B（2，2，0），
$\overrightarrow{BC}=（-2，0，0）$，$\overrightarrow{PC}=（0，2，-2）$，$\overrightarrow{PA}=（1，0，-2）$
设平面PBC的法向量为：$\overrightarrow{n}=（x，y，z）$，
由$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{BC}=0\\ \overrightarrow{n}•\overrightarrow{PC}=0\end{array}\right.$，
整理得：$\left\{\begin{array}{l}-2x=0\\ 2y-2z=0\end{array}\right.$，
解得：$\overrightarrow{n}=（0，1，1）$，
所以：sinθ=cos$＜\overrightarrow{n}，\overrightarrow{PA}＞$=$\left|\frac{\overrightarrow{PA}•\overrightarrow{n}}{\left|\overrightarrow{n}\right|\left|\overrightarrow{PA}\right|}\right|=\frac{\sqrt{10}}{5}$．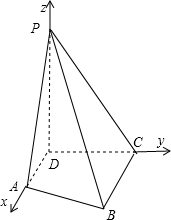

点评 本题考查的知识要点：线面垂直的判定和性质的应用，空间直角坐标系，法向量的应用，线面的夹角的应用．