
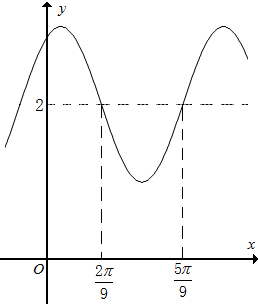
 函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$.
函数y=Asin(ωx+φ)+2(A>0,ω>0,0<φ<2π)的图象如图所示,则ω=3,φ=$\frac{π}{3}$. 分析 首先根据函数的图象得到最小正周期T,进而根据周期公式可求ω,再根据平衡点利用五点作图法求出φ,即可得解.
解答 解:∵由函数图象可知,T=2($\frac{5π}{9}$-$\frac{2π}{9}$)=$\frac{2π}{3}$,
∴ω=$\frac{2π}{T}$=3,
∵函数图象过点($\frac{2π}{9}$,2),
∴Asin(3×$\frac{2π}{9}$+φ)+2=2,由五点法作图可得:3×$\frac{2π}{9}$+φ=π,
∴解得:φ=$\frac{π}{3}$.
故答案为:3,$\frac{π}{3}$.
点评 解决此类问题的关键是求φ,首先根据函数的图象得到ω,再根据最值点或者平衡点求出所有的φ,进而根据φ的范围求出答案即可,注意在代入已知点时最好代入最值点,因为在一个周期内只有一个最大值,一个最小值,而平衡点却有两个,假如代入的是平衡点则需要根据函数的单调性再来判定φ的取值.


科目:高中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.2 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | p∧q | C. | p∨¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com