练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知向量
    a
    =（cos
    3x
    2
    ，sin
    3x
    2
    ），
    b
    =（cos
    x
    2
    ，-sin
    x
    2
    ），且x∈[0，
    π
    2
    ]．
    （1）求
    a
    •
    b
    及|
    a
    +
    b
    |；
    （2）若f（x）=
    a
    •
    b
    -2λ|
    a
    +
    b
    |的最小值为-7，求实数λ的值．
    考点：两角和与差的正弦函数,平面向量数量积的运算,三角函数的最值
    专题：三角函数的求值
    分析：（1）由数量积的运算和模长的计算，结合三角函数运算可得；
    （2）由（1）可知f（x）=2（cosx-λ）2-2λ2-1，由x∈[0，
    π
    2
    ]可得cosx∈[0，1]，由二次函数区间的最值分类讨论可得．
    解答： 解：（1）∵
    a
    =（cos
    3x
    2
    ，sin
    3x
    2
    ），
    b
    =（cos
    x
    2
    ，-sin
    x
    2
    ），
    ∴
    a
    •
    b
    =cos
    3x
    2
    cos
    x
    2
    -sin
    3x
    2
    sin
    x
    2
    =cos（
    3x
    2
    +
    x
    2
    ）=cos2x，
    ∴|
    a
    +
    b
    |2=
    a
    2    +
    b
    2    +2
    a
    •
    b
    =cos2
    3x
    2
    +sin2
    3x
    2
    +cos2
    x
    2
    +sin2
    x
    2
    +2cos2x
    =2+2cos2x=4cos2x，又x∈[0，
    π
    2
    ]，∴|
    a
    +
    b
    |=2cosx；
    （2）由（1）可知f（x）=
    a
    •
    b
    -2λ|
    a
    +
    b
    |=cos2x-4λcosx
    =2cos2x-4λcosx-1=2（cosx-λ）2-2λ2-1，
    ∵x∈[0，
    π
    2
    ]，∴cosx∈[0，1]，
    当λ≤0时，由二次函数可知cosx=0时f（x）取最小值-1，这与最小值为-7矛盾；
    当λ≥1时，由二次函数可知cosx=1时f（x）取最小值1-4λ=-7，解得λ=2，符合题意；
    当0＜λ＜1时，由二次函数可知cosx=λ时f（x）取最小值-2λ2-1=-7，解得λ=±
    		3
    ，这与0＜λ＜1矛盾；
    综上可知实数λ的值为2
    点评：本题考查两角和与差的三角函数，涉及向量的运算和二次函数区间的最值以及分类讨论的思想，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

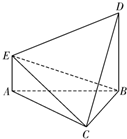    如图，在多面体ABCDE中，DB丄平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，AE=1，BD=2．
    （Ⅰ）在线段DC上存在一点F，使得EF丄面DBC，试确定F的位置，并证明你的结论；
    （Ⅱ）求二面角D-EC-B的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，已知
    a
    、
    b
    是互相垂直的两个单位向量，点Q满足
    OQ
    =3
    a
    +4
    b
    ．曲线C={P|
    OP
    =2
    a
    cosθ+2
    b
    sinθ，0≤θ≤2π}，区域Ω={P|0＜r≤|
    PQ
    |≤R，r＜R}．若C∩Ω=C，则（　　）
    A、0＜r≤3且R≥7
    B、0＜r≤3≤R≤7
    C、0＜r≤5＜R＜7
    D、5≤r＜7≤R

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在几何体ABCDE中，平面ABC⊥平面BCD，AE∥BD，△ABC为边长等于2的正三角形，CD=2
    		3
    ，BD=4，M为CD的中点．
    （Ⅰ）证明：平面ECD⊥平面ABC；
    （Ⅱ）求二面角C-AB-M的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在四面体ABCD中，E、F分别是AD、BC中，AB=CD=2，EF=
    		2
    ．求异面直线中AB、CD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（x2+bx+b）ex的极值点为x=-
    2
    3
    和x=1．
    （1）当b=1时，求函数f（x）的增区间；
    （2）当0＜b≤2时，求函数f（x）在[-2b，b]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

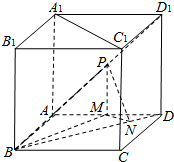    如图，正方体ABCD-A1B1C1D1的棱长为2，点P为面ADD1A1的对角线AD1的中点．PM⊥平面ABCD交AD与M，MN⊥BD于N．
    （1）求异面直线PN与A1C1所成角的大小；（结果可用反三角函数值表示）
    （2）求三棱锥P-BMN的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    小明每天起床后要做如下事情：洗漱5分钟，收拾床褥4分钟，听广播15分钟，吃早饭8分钟．要完成这些事情，小明要花费的最少时间为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在锐角△ABC中，a、b、c分别为内角A、B、C所对的边长，且满足
    sinA
    a
    =
    		3
    2b
    ．
    （1）求∠B的大小；
    （2）若b=
    		7
    ，△ABC的面积S△ABC=
    3
    		3
    4
    ，求a+c的值．

    查看答案和解析>>

    同步练习册答案