
【题目】将![]() 棋盘的每个方格都随意染黑白两色之一,每次操作是将其中同行、同列、同对角线的连续五个方格改变成相反的颜色.试问:能否经过有限次操作,使得所有方格的颜色都变成与原先相反的颜色?
棋盘的每个方格都随意染黑白两色之一,每次操作是将其中同行、同列、同对角线的连续五个方格改变成相反的颜色.试问:能否经过有限次操作,使得所有方格的颜色都变成与原先相反的颜色?
【答案】见解析
【解析】
当![]() 时,目标可以实现;当
时,目标可以实现;当![]() 时,目标不可以实现.
时,目标不可以实现.
(1)如果![]() ,可由5是质数,不妨设
,可由5是质数,不妨设![]() ,则
,则![]() 棋盘可划分为若干个
棋盘可划分为若干个![]() 的矩形,对每一个
的矩形,对每一个![]() 的矩形操作一次即可.
的矩形操作一次即可.
(2)如果![]() ,可设
,可设![]() ,
,![]() (
(![]() 、
、![]() ).
).
将![]() 棋盘的方格用1、2、3、4、5编号,使每一行每一列的数都构成周期为5的周期数列,其左上角
棋盘的方格用1、2、3、4、5编号,使每一行每一列的数都构成周期为5的周期数列,其左上角![]() 棋盘的编号如图.
棋盘的编号如图.

因为图中每行、每列的数都是以5为周期的周期数列,所以,同行、同列、同对角线的连续5个数都恰好包含1、2、3、4、5各1个.故每次操作都使每一类编号的方格中恰有一个方格改变了一次颜色.
用![]() 表示编号为
表示编号为![]() 的方格颜色改变的次数和(
的方格颜色改变的次数和(![]() ),则每次操作,各
),则每次操作,各![]() 同时增加1,于是,操作中恒有
同时增加1,于是,操作中恒有![]() .
.
若所有方格的颜色都变成与原先颜色相反,则每个方格颜色改变的次数为奇数.
考察棋盘左上角![]() 子棋盘的编号,对任何
子棋盘的编号,对任何![]() 、
、![]() (
(![]() 、
、![]() ),在
),在![]() 子棋盘中一定存在一个编号
子棋盘中一定存在一个编号![]() 与一个编号
与一个编号![]() (
(![]() 、
、![]() ),使得
),使得![]() 出现的次数比
出现的次数比![]() 出现的次数多一次(逐一验证
出现的次数多一次(逐一验证![]() 子棋盘即可).
子棋盘即可).
去掉此![]() 子棋盘,则
子棋盘,则![]() 棋盘的剩余部分各编号出现的次数相等.于是,整个
棋盘的剩余部分各编号出现的次数相等.于是,整个![]() 棋盘中编号
棋盘中编号![]() 、
、![]() 的个数一个为奇数、一个为偶数.由于每个方格都改变奇数次颜色,从而,
的个数一个为奇数、一个为偶数.由于每个方格都改变奇数次颜色,从而,![]() 、
、![]() 一个为奇数个奇数的和、一个为偶数个奇数的和,也即
一个为奇数个奇数的和、一个为偶数个奇数的和,也即![]() 、
、![]() 一为奇数、一为偶数.于是,
一为奇数、一为偶数.于是,![]() ,矛盾.
,矛盾.
故不可能所有方格的颜色都变成与原先相反的颜色.


科目:高中数学 来源: 题型:
【题目】设![]() 为不同的两点,直线
为不同的两点,直线![]() ,下列命题正确的有( ).
,下列命题正确的有( ).
①不论![]() 为何值,点
为何值,点![]() 都不在直线
都不在直线![]() 上;
上;
②若![]() ,则过点
,则过点![]() 的直线与直线
的直线与直线![]() 平行;
平行;
③若![]() ,则直线
,则直线![]() 经过
经过![]() 的中点;
的中点;
④若![]() ,则点
,则点![]() 在直线
在直线![]() 的同侧且直线
的同侧且直线![]() 与线段
与线段![]() 的延长线相交.
的延长线相交.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的实轴端点分别为
的实轴端点分别为![]() ,记双曲线的其中一个焦点为
,记双曲线的其中一个焦点为![]() ,一个虚轴端点为
,一个虚轴端点为![]() ,若在线段
,若在线段![]() 上(不含端点)有且仅有两个不同的点
上(不含端点)有且仅有两个不同的点![]() ,使得
,使得![]() ,则双曲线的离心率
,则双曲线的离心率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
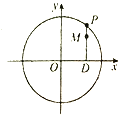
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数![]() 模型.园区服务中心P在x轴正半轴上,PO=
模型.园区服务中心P在x轴正半轴上,PO=![]() 百米.
百米.

(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道直线段PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,过抛物线![]() 上一定点
上一定点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() .
.

(1)求该抛物线上纵坐标为![]() 的点到其焦点
的点到其焦点![]() 的距离;
的距离;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值,并证明直线
的值,并证明直线![]() 的斜率是非零常数.
的斜率是非零常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的各棱长均为2,
的各棱长均为2, ![]() 面
面![]() ,E,F分别为棱
,E,F分别为棱![]() 的中点.
的中点.
(1)求证:直线BE∥平面![]() ;
;
(2)平面![]() 与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥
与直线AB交于点M,指出点M的位置,说明理由,并求三棱锥![]() 的体积.
的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com