
ΓΨΧβΡΩΓΩ…ΫΕΪ Γ2020ΡξΗΏΩΦΫΪ Β ©–¬ΒΡΗΏΩΦΗΡΗοΖΫΑΗ.ΩΦ…ζΒΡΗΏΩΦΉή≥…Φ®ΫΪ”…3Ο≈Ά≥“ΜΗΏΩΦΩΤΡΩ≥…Φ®ΚΆΉ‘÷ς―Γ‘ώΒΡ3Ο≈Τ’Ά®ΗΏ÷–―ß“ΒΥ°ΤΫΒ»ΦΕΩΦ ‘ΩΤΡΩ≥…Φ®Ήι≥…Θ§ΉήΖ÷ΈΣ750Ζ÷.Τδ÷–Θ§Ά≥“ΜΗΏΩΦΩΤΡΩΈΣ”οΈΡΓΔ ΐ―ßΓΔΆβ”οΘ§Ή‘÷ς―Γ‘ώΒΡ3Ο≈Τ’Ά®ΗΏ÷–―ß“ΒΥ°ΤΫΒ»ΦΕΩΦ ‘ΩΤΡΩ «¥”ΈοάμΓΔΜ·―ßΓΔ…ζΈοΓΔάζ ΖΓΔ’ΰ÷ΈΓΔΒΊάμ6ΩΤ÷–―Γ‘ώ3Ο≈ΉςΈΣ―ΓΩΦΩΤΡΩΘ§”οΓΔ ΐΓΔΆβ»ΐΩΤΗς’Φ150Ζ÷Θ§―ΓΩΦΩΤΡΩ≥…Φ®≤…”ΟΓΑΗ≥Ζ÷÷ΤΓ±Θ§Φ¥‘≠ ΦΖ÷ ΐ≤Μ÷±Ϋ””ΟΘ§Εχ «Α¥’’―ß…ζΖ÷ ΐ‘Ύ±ΨΩΤΡΩΩΦ ‘ΒΡ≈≈Οϊά¥Μ°Ζ÷Β»ΦΕ≤Δ“‘¥Υ¥ρΖ÷ΒΟΒΫΉνΚσΒΟΖ÷.ΗυΨίΗΏΩΦΉέΚœΗΡΗοΖΫΑΗΘ§ΫΪΟΩΟ≈Β»ΦΕΩΦ ‘ΩΤΡΩ÷–ΩΦ…ζΒΡ‘≠ Φ≥…Φ®¥”ΗΏΒΫΒΆΖ÷ΈΣ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Ι≤8ΗωΒ»ΦΕΓΘ≤Έ’’’ΐΧ§Ζ÷≤Φ‘≠‘ρΘ§»ΖΕ®ΗςΒ»ΦΕ»Υ ΐΥυ’Φ±»άΐΖ÷±πΈΣ
Ι≤8ΗωΒ»ΦΕΓΘ≤Έ’’’ΐΧ§Ζ÷≤Φ‘≠‘ρΘ§»ΖΕ®ΗςΒ»ΦΕ»Υ ΐΥυ’Φ±»άΐΖ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() .Β»ΦΕΩΦ ‘ΩΤΡΩ≥…Φ®ΦΤ»κΩΦ…ζΉή≥…Φ® ±Θ§ΫΪ
.Β»ΦΕΩΦ ‘ΩΤΡΩ≥…Φ®ΦΤ»κΩΦ…ζΉή≥…Φ® ±Θ§ΫΪ![]() ÷Ν
÷Ν![]() Β»ΦΕΡΎΒΡΩΦ…ζ‘≠ Φ≥…Φ®Θ§“ά’’Β»±»άΐΉΣΜΜΖ®‘ρΘ§Ζ÷±πΉΣΜΜΒΫ91-100ΓΔ81-90ΓΔ71-80Θ§61-70ΓΔ51-60ΓΔ41-50ΓΔ31-40ΓΔ21-30ΑΥΗωΖ÷ ΐ«χΦδΘ§ΒΟΒΫΩΦ…ζΒΡΒ»ΦΕ≥…Φ®.
Β»ΦΕΡΎΒΡΩΦ…ζ‘≠ Φ≥…Φ®Θ§“ά’’Β»±»άΐΉΣΜΜΖ®‘ρΘ§Ζ÷±πΉΣΜΜΒΫ91-100ΓΔ81-90ΓΔ71-80Θ§61-70ΓΔ51-60ΓΔ41-50ΓΔ31-40ΓΔ21-30ΑΥΗωΖ÷ ΐ«χΦδΘ§ΒΟΒΫΩΦ…ζΒΡΒ»ΦΕ≥…Φ®.
ΨΌάΐΥΒΟς.
Ρ≥Ά§―ßΜ·―ß―ßΩΤ‘≠ ΦΖ÷ΈΣ65Ζ÷Θ§ΗΟ―ßΩΤ![]() Β»ΦΕΒΡ‘≠ ΦΖ÷Ζ÷≤Φ«χΦδΈΣ58ΓΪ69Θ§‘ρΗΟΆ§―ßΜ·―ß―ßΩΤΒΡ‘≠ Φ≥…Φ® τ
Β»ΦΕΒΡ‘≠ ΦΖ÷Ζ÷≤Φ«χΦδΈΣ58ΓΪ69Θ§‘ρΗΟΆ§―ßΜ·―ß―ßΩΤΒΡ‘≠ Φ≥…Φ® τ![]() Β»ΦΕ.Εχ
Β»ΦΕ.Εχ![]() Β»ΦΕΒΡΉΣΜΜΖ÷«χΦδΈΣ61ΓΪ70Θ§Ρ«Ο¥ΗΟΆ§―ßΜ·―ß―ßΩΤΒΡΉΣΜΜΖ÷ΈΣΘΚ
Β»ΦΕΒΡΉΣΜΜΖ÷«χΦδΈΣ61ΓΪ70Θ§Ρ«Ο¥ΗΟΆ§―ßΜ·―ß―ßΩΤΒΡΉΣΜΜΖ÷ΈΣΘΚ
…ηΗΟΆ§―ßΜ·―ßΩΤΒΡΉΣΜΜΒ»ΦΕΖ÷ΈΣ![]() Θ§
Θ§![]() Θ§«σΒΟ
Θ§«σΒΟ![]() .
.
ΥΡ…αΈε»κΚσΗΟΆ§―ßΜ·―ß―ßΩΤΗ≥Ζ÷≥…Φ®ΈΣ67.
Θ®1Θ©Ρ≥–ΘΗΏ“ΜΡξΦΕΙ≤2000»ΥΘ§ΈΣΗχΗΏ“Μ―ß…ζΚœάμ―ΓΩΤΧαΙ©“άΨίΘ§Ε‘ΝυΗω―ΓΩΦΩΤΡΩΫχ––≤β ‘Θ§Τδ÷–ΈοάμΩΦ ‘‘≠ Φ≥…Φ®Μυ±ΨΖΰ¥”’ΐΧ§Ζ÷≤Φ![]() .
.
Θ®iΘ©»τ–ΓΟςΆ§―ß‘Ύ’β¥ΈΩΦ ‘÷–Έοάμ‘≠ ΦΖ÷ΈΣ84Ζ÷Θ§Β»ΦΕΈΣ![]() Θ§ΤδΥυ‘Ύ‘≠ ΦΖ÷Ζ÷≤Φ«χΦδΈΣ82ΓΪ93Θ§«σ–ΓΟςΉΣΜΜΚσΒΡΈοάμ≥…Φ®ΘΜ
Θ§ΤδΥυ‘Ύ‘≠ ΦΖ÷Ζ÷≤Φ«χΦδΈΣ82ΓΪ93Θ§«σ–ΓΟςΉΣΜΜΚσΒΡΈοάμ≥…Φ®ΘΜ
Θ®iiΘ©«σΈοάμ‘≠ ΦΖ÷‘Ύ«χΦδ![]() ΒΡ»Υ ΐΘΜ
ΒΡ»Υ ΐΘΜ
Θ®2Θ©Α¥ΗΏΩΦΗΡΗοΖΫΑΗΘ§»τ¥”»Ϊ ΓΩΦ…ζ÷–ΥφΜζ≥ι»Γ4»ΥΘ§Φ«![]() ±μ Ψ’β4»Υ÷–Β»ΦΕ≥…Φ®‘Ύ«χΦδ
±μ Ψ’β4»Υ÷–Β»ΦΕ≥…Φ®‘Ύ«χΦδ![]() ΒΡ»Υ ΐΘ§«σ
ΒΡ»Υ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
Θ®ΗΫΘΚ»τΥφΜζ±δΝΩ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ©
Θ©
ΓΨ¥πΑΗΓΩ(1)Θ®iΘ©83.;Θ®iiΘ©272.(2)ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί‘≠ ΦΖ÷ ΐΖ÷≤Φ«χΦδΦΑΉΣΜΜΖ÷«χΦδΘ§ΫαΚœΥυΗχ ΨάΐΘ§Φ¥Ω…«σΒΟ–ΓΟςΉΣΜΜΚσΒΡΈοάμ≥…Φ®ΘΜΗυΨί’ΐΧ§Ζ÷≤Φ¬ζΉψ![]() Θ§ΫαΚœ’ΐΧ§Ζ÷≤ΦΒΡΕ‘≥Τ–‘Φ¥Ω…«σΒΟ
Θ§ΫαΚœ’ΐΧ§Ζ÷≤ΦΒΡΕ‘≥Τ–‘Φ¥Ω…«σΒΟ![]() ΡΎΒΡΗ≈¬ Θ§ΗυΨίΉή»Υ ΐΦ¥Ω…«σΒΟ‘ΎΗΟ«χΦδΒΡ»Υ ΐΓΘ
ΡΎΒΡΗ≈¬ Θ§ΗυΨίΉή»Υ ΐΦ¥Ω…«σΒΟ‘ΎΗΟ«χΦδΒΡ»Υ ΐΓΘ
Θ®2Θ©ΗυΨίΗςΒ»ΦΕ»Υ ΐΥυ’Φ±»άΐΩ…÷Σ‘Ύ«χΦδ![]() ΡΎΒΡΗ≈¬ ΈΣ
ΡΎΒΡΗ≈¬ ΈΣ![]() Θ§”…ΕΰœνΖ÷≤ΦΦ¥Ω…«σΒΟ
Θ§”…ΕΰœνΖ÷≤ΦΦ¥Ω…«σΒΟ![]() ΒΡΖ÷≤ΦΝ–ΦΑΗς«ιΩωœ¬ΒΡΗ≈¬ Θ§ΫαΚœ ΐ―ßΤΎΆϊΒΡΙΪ ΫΦ¥Ω…«σΫβΓΘ
ΒΡΖ÷≤ΦΝ–ΦΑΗς«ιΩωœ¬ΒΡΗ≈¬ Θ§ΫαΚœ ΐ―ßΤΎΆϊΒΡΙΪ ΫΦ¥Ω…«σΫβΓΘ
Θ®1Θ©Θ®iΘ©…η–ΓΟςΉΣΜΜΚσΒΡΈοάμΒ»ΦΕΖ÷ΈΣ![]() Θ§
Θ§
![]() Θ§
Θ§
«σΒΟ![]() .
.
–ΓΟςΉΣΜΜΚσΒΡΈοάμ≥…Φ®ΈΣ83Ζ÷ΘΜ
Θ®iiΘ©“ρΈΣΈοάμΩΦ ‘‘≠ ΦΖ÷Μυ±ΨΖΰ¥”’ΐΧ§Ζ÷≤Φ![]() Θ§
Θ§
Υυ“‘![]()
![]()
![]()
![]() .
.
Υυ“‘Έοάμ‘≠ ΦΖ÷‘Ύ«χΦδ![]() ΒΡ»Υ ΐΈΣ
ΒΡ»Υ ΐΈΣ![]() Θ®»ΥΘ©ΘΜ
Θ®»ΥΘ©ΘΜ
Θ®2Θ©”…Χβ“βΒΟΘ§ΥφΜζ≥ι»Γ1»ΥΘ§ΤδΒ»ΦΕ≥…Φ®‘Ύ«χΦδ![]() ΡΎΒΡΗ≈¬ ΈΣ
ΡΎΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§
ΥφΜζ≥ι»Γ4»ΥΘ§‘ρ![]() .
.
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
![]() .
.
![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
ΐ―ßΤΎΆϊ![]() .
.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() .
.
Θ®1Θ©«σfΘ®xΘ©ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©Β±xΘΨ0 ±Θ§ex©¹ax2©¹x©¹aΓί0≥…ΝΔΘ§«σ’ΐ Β ΐaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§“―÷Σ![]() «’ΐ»ΐΫ«–ΈΘ§»τ
«’ΐ»ΐΫ«–ΈΘ§»τ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§ΤΫΟφ
Θ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§«“
Θ§«“![]() Θ°
Θ°
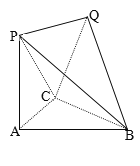
Θ®1Θ©«σ÷ΛΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§«σΕΰΟφΫ«
Θ§«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷ΒΘ°
ΒΡ”ύœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΪ≈ΠœΏΉν‘γ”Ύ1694Ρξ±Μ»π Ω ΐ―ßΦ“―≈Ης≤ΦΓΛ≤°≈§άϊ”Οά¥Οη ωΥϊΥυΖΔœ÷ΒΡ«ζœΏ.‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Α―ΒΫΕ®Βψ
÷–Θ§Α―ΒΫΕ®Βψ![]() Θ§
Θ§![]() Ψύάκ÷°ΜΐΒ»”Ύ
Ψύάκ÷°ΜΐΒ»”Ύ![]() ΒΡΒψΒΡΙλΦΘ≥ΤΈΣΥΪ≈ΠœΏ
ΒΡΒψΒΡΙλΦΘ≥ΤΈΣΥΪ≈ΠœΏ![]() .“―÷ΣΒψ
.“―÷ΣΒψ![]() «ΥΪ≈ΠœΏ
«ΥΪ≈ΠœΏ![]() …œ“ΜΒψΘ§œ¬Ν–ΥΒΖ®÷–’ΐ»ΖΒΡ”–Θ® Θ©
…œ“ΜΒψΘ§œ¬Ν–ΥΒΖ®÷–’ΐ»ΖΒΡ”–Θ® Θ©
ΔΌΥΪ≈ΠœΏΨ≠Ιΐ‘≠Βψ![]() ΘΜ ΔΎΥΪ≈ΠœΏ
ΘΜ ΔΎΥΪ≈ΠœΏ![]() ΙΊ”Ύ‘≠Βψ
ΙΊ”Ύ‘≠Βψ![]() ÷––ΡΕ‘≥ΤΘΜ
÷––ΡΕ‘≥ΤΘΜ
Δέ![]() ΘΜ ΔήΥΪ≈ΠœΏ
ΘΜ ΔήΥΪ≈ΠœΏ![]() …œ¬ζΉψ
…œ¬ζΉψ![]() ΒΡΒψ
ΒΡΒψ![]() ”–ΝΫΗω.
”–ΝΫΗω.
A.ΔΌΔΎB.ΔΌΔΎΔέC.ΔΎΔέD.ΔΎΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]()
Θ®1Θ©»τ![]() Θ§«“
Θ§«“![]() ‘ΎΤδΕ®“ε”ρ…œ¥φ‘ΎΒΞΒςΒίΦθ«χΦδΘ§«σ Β ΐ
‘ΎΤδΕ®“ε”ρ…œ¥φ‘ΎΒΞΒςΒίΦθ«χΦδΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©…ηΚ· ΐ![]() Θ§
Θ§ ![]() Θ§»τ
Θ§»τ![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() ”κΚ· ΐ
”κΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§ΙΐœΏΕΈ
Θ§ΙΐœΏΕΈ![]() ΒΡ÷–ΒψΉς
ΒΡ÷–ΒψΉς![]() ÷αΒΡ¥ΙœΏΖ÷±πΫΜ
÷αΒΡ¥ΙœΏΖ÷±πΫΜ![]() Θ§
Θ§ ![]() ”ΎΒψ
”ΎΒψ![]() ΓΔ
ΓΔ![]() Θ§÷ΛΟςΘΚ
Θ§÷ΛΟςΘΚ ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ”κ
¥ΠΒΡ«–œΏ”κ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ≤ΜΤΫ––.
¥ΠΒΡ«–œΏ≤ΜΤΫ––.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§«ζœΏ
÷–Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ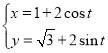 Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§
ΈΣ≤Έ ΐΘ©Θ§“‘Ήχ±ξ‘≠ΒψΈΣΦΪΒψΘ§![]() ÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ
÷α’ΐΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§÷±œΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ§«“«ζœΏ
Θ§«“«ζœΏ![]() ΙΊ”Ύ÷±œΏ
ΙΊ”Ύ÷±œΏ![]() Ε‘≥ΤΘ°
Ε‘≥ΤΘ°
Θ®1Θ©«σ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() Θ§
Θ§![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΘΚ
ΘΚ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() ΒΡΟφΜΐ≤Μ≥§Ιΐ
ΒΡΟφΜΐ≤Μ≥§Ιΐ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ΒΡ«ψ–±Ϋ«ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ«ψ–±Ϋ«ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®÷–’ΐ»ΖΒΡ «Θ® Θ©
A.Ε‘ΨΏ”–œΏ–‘œύΙΊΙΊœΒΒΡ±δΝΩ![]() ”–“ΜΉιΙέ≤β ΐΨί
”–“ΜΉιΙέ≤β ΐΨί![]() Θ§ΤδœΏ–‘ΜΊΙιΖΫ≥Χ «
Θ§ΤδœΏ–‘ΜΊΙιΖΫ≥Χ «![]() Θ§«“
Θ§«“![]() Θ§‘ρ Β ΐ
Θ§‘ρ Β ΐ![]() ΒΡ÷Β «
ΒΡ÷Β «![]()
B.’ΐΧ§Ζ÷≤Φ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() ΚΆ
ΚΆ![]() …œ»Γ÷ΒΒΡΗ≈¬ œύΒ»
…œ»Γ÷ΒΒΡΗ≈¬ œύΒ»
C.»τΝΫΗωΥφΜζ±δΝΩΒΡœΏ–‘œύΙΊ–‘‘Ϋ«ΩΘ§‘ρœύΙΊœΒ ΐ![]() ΒΡ÷Β‘ΫΫ”Ϋϋ”Ύ1
ΒΡ÷Β‘ΫΫ”Ϋϋ”Ύ1
D.»τ“ΜΉι ΐΨί![]() ΒΡΤΫΨυ ΐ «2Θ§‘ρ’βΉι ΐΨίΒΡ÷Ύ ΐΚΆ÷–ΈΜ ΐΕΦ «2
ΒΡΤΫΨυ ΐ «2Θ§‘ρ’βΉι ΐΨίΒΡ÷Ύ ΐΚΆ÷–ΈΜ ΐΕΦ «2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©Β±a=-2 ±Θ§«σΚ· ΐf(x)ΒΡΦΪ÷ΒΘΜ
Θ®2Θ©»τln[e(x+1)]Γί2- f(-x)Ε‘»Έ“βΒΡxΓ [0Θ§+Γό)≥…ΝΔΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σάβ≥ΛΈΣ2ΒΡ’ΐΖΫΧε![]() ÷–Θ§EΈΣDC÷–ΒψΘ§F‘ΎœΏΕΈ
÷–Θ§EΈΣDC÷–ΒψΘ§F‘ΎœΏΕΈ![]() …œ‘ΥΕ·Θ§‘ρ»ΐάβΉΕ
…œ‘ΥΕ·Θ§‘ρ»ΐάβΉΕ![]() ΒΡΆβΫ”«ρΒΡ±μΟφΜΐΉν–Γ÷ΒΈΣΘ® Θ©
ΒΡΆβΫ”«ρΒΡ±μΟφΜΐΉν–Γ÷ΒΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com