
分析 (Ⅰ)根据导函数的概念可得f'(1)=0,代入求出a,利用导函数的正负判断函数的单调性即可;
(Ⅱ)|f(cosθ)-f(sinθ)|≤m恒成立,只需求出左式的最大值即可,根据(1)式得出函数的单调性,求出函数的最大值,最小值进而得出|f(cosθ)-f(sinθ)|的最大值,求出m的取值范围.
解答 解:(Ⅰ)f′(x)=ex(ax2+x+1+2ax+1).由条件知,f′(1)=0,
∴a+3+2a=0,
∴a=-1.
∴f′(x)=ex(-x2-x+2)=-ex(x+2)(x-1).
故当x∈(-∞,-2)∪(1,+∞)时,f′(x)<0;
当x∈(-2,1)时,f′(x)>0.
∴f(x)在(-∞,-2),(1,+∞)单调减少,在(-2,1)单调增加;(6分)
(Ⅱ)由(Ⅰ)知f(x)在[0,1]单调增加,
故f(x)在[0,1]的最大值为f(1)=e,最小值为f(0)=1.
从而对任意x1,x2∈[0,1],有|f(x1)-f(x2)|≤e-1.(10分)
而当$θ∈[0,\frac{π}{2}]$时,cosθ,sinθ∈[0,1].
从而|f(cosθ)-f(sinθ)|≤e-1,
所以m≥e-1…(12分)
点评 考查了导函数的概念,利用导函数判断函数的单调性,对恒成立问题的转化.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 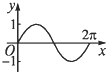 | B. | 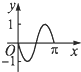 | C. | 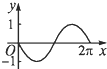 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com