
分析 (Ⅰ)由条件利用同角三角函数的基本关系求得sinα的值.
(Ⅱ)由条件诱导公式,求得要求式子的值.
解答 解:(Ⅰ)∵cosα=-$\frac{\sqrt{5}}{5}$,α∈($\frac{π}{2}$,π),∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{2\sqrt{5}}{5}$.
(Ⅱ)$\frac{sin(\frac{3π}{2}+α)+2cos(\frac{π}{2}+α)}{cos(3π-α)}$=$\frac{-cosα-2sinα}{-cosα}$=$\frac{cosα+2sinα}{cosα}$=$\frac{-\frac{\sqrt{5}}{5}+2•\frac{2\sqrt{5}}{5}}{-\frac{\sqrt{5}}{5}}$=-3.
点评 本题主要考查同角三角函数的基本关系,诱导公式的应用,属于基础题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨(¬q) | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
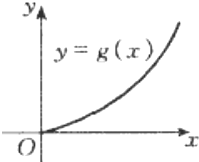
| A. | 0<g′(2)<g′(3)<g(3)-g(2) | B. | 0<g′(3)<g(3)-g(2)<g′(2) | C. | 0<g′(2)<g(3)-g(2)<g′(3) | D. | 0<g(3)-g(2)<g′(2)<g′(3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com