
【题目】我国的“洋垃极禁止入境”政策已实施一年多![]() 某沿海地区的海岸线为一段圆弧AB,对应的圆心角
某沿海地区的海岸线为一段圆弧AB,对应的圆心角![]() ,该地区为打击洋垃圾走私,在海岸线外侧20海里内的海域ABCD对不明船只进行识别查证
,该地区为打击洋垃圾走私,在海岸线外侧20海里内的海域ABCD对不明船只进行识别查证![]() 如图:其中海域与陆地近似看作在同一平面内
如图:其中海域与陆地近似看作在同一平面内![]() 在圆弧的两端点A,B分别建有监测站,A与B之间的直线距离为100海里.
在圆弧的两端点A,B分别建有监测站,A与B之间的直线距离为100海里.
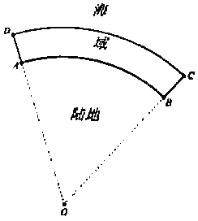
![]() 求海域ABCD的面积;
求海域ABCD的面积;
![]() 现海上P点处有一艘不明船只,在A点测得其距A点40海里,在B点测得其距B点
现海上P点处有一艘不明船只,在A点测得其距A点40海里,在B点测得其距B点![]() 海里
海里![]() 判断这艘不明船只是否进入了海域ABCD?请说明理由.
判断这艘不明船只是否进入了海域ABCD?请说明理由.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 xOy中,O为坐标原点,已知点![]() ,P是动点,且三角形POQ的三边所在直线的斜率满足
,P是动点,且三角形POQ的三边所在直线的斜率满足![]() .
.
(1)求点P的轨迹C的方程;
(2)过F作倾斜角为60°的直线L,交曲线C于A,B两点,求△AOB的面积;
(3)过点![]() 任作两条互相垂直的直线
任作两条互相垂直的直线![]() ,分别交轨迹 C 于点A,B和M,N,设线段AB,MN的中点分别为E,F.,求证:直线EF恒过一定点.
,分别交轨迹 C 于点A,B和M,N,设线段AB,MN的中点分别为E,F.,求证:直线EF恒过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]()
(1)求以椭圆C的焦点为顶点,顶点为焦点的椭圆方程;
(2)过椭圆C的左焦点且倾斜角为![]() 的直线与椭圆交于A,B两点,求
的直线与椭圆交于A,B两点,求![]() 的面积;
的面积;
(3)过定点![]() 的直线交椭圆C于AB两点,求弦AB中点P的轨迹方程.
的直线交椭圆C于AB两点,求弦AB中点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过动点![]() 的直线交
的直线交![]() 轴与点
轴与点![]() ,交
,交![]() 于点
于点![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点.过点
的中点.过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于另一点
于另一点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)设直线![]() 的斜率分别为
的斜率分别为![]() ,证明
,证明![]() 为定值;
为定值;
(ⅱ)求直线![]() 的斜率的最小值.
的斜率的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
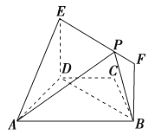
(1)求证:AD⊥平面BFED;
(2)点P在线段EF上运动,设平面PAB与平面ADE所成锐二面角为θ,试求θ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(1)若过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 方程;
方程;
(2)在(1)的条件下,若直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 轴上是否存在点
轴上是否存在点![]() 使
使![]() (
(![]() 为坐标原点)?若存在,求出点
为坐标原点)?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com