
| A. | 2$\sqrt{3}$ | B. | 1 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 依次计算|$\overrightarrow{a}$|,$\overrightarrow{a}•\overrightarrow{b}$,$(\overrightarrow{a}-\overrightarrow{b})^{2}$,将$(\overrightarrow{a}-\overrightarrow{b})^{2}$开方即可.
解答 解:|$\overrightarrow{a}$|=1,∴$\overrightarrow{a}•\overrightarrow{b}$=1×$\sqrt{3}×$cos30°=$\frac{3}{2}$.
∴($\overrightarrow{a}-\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=1.
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}-\overrightarrow{b})^{2}}$=1.
故选:B.
点评 本题考查了平面向量的数量积运算,属于基础题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2014 | C. | 4029 | D. | 4028 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
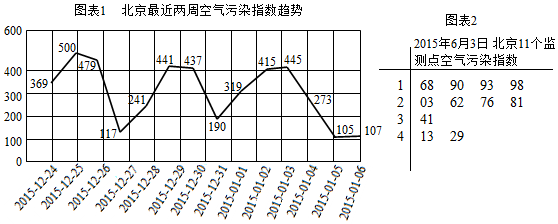
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,x02-x0>0”的否定是“?x0∈R,x02-x0<0” | |
| B. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 | |
| C. | 在回归直线$\widehat{y}$=-0.5x+3中,当解释变量x每增加一个单位时,预报变量$\widehat{y}$平均减少0.5个单位 | |
| D. | 若a,b∈[0,2],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知AB是圆O的直径,AB=2,点C在直径AB的延长线上,BC=1,点P是圆O上半圆上的动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,记∠POB=x,将△OPC和△PCD的面积之和表示成x的函数f(x),则y=f(x)取最大值时x的值为( )
如图,已知AB是圆O的直径,AB=2,点C在直径AB的延长线上,BC=1,点P是圆O上半圆上的动点,以PC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,记∠POB=x,将△OPC和△PCD的面积之和表示成x的函数f(x),则y=f(x)取最大值时x的值为( )| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com