
分析 通过P为真,求出实数a的取值范围;通过Q为真,求实数a的取值范围,通过P∧Q为假命题,P∨Q为真命题,分类讨论求出求实数a的取值范围.
解答 解:P真,(1-x)ax<1恒成立?ax2-ax+1>0恒成立,
(1)a=0时,恒成立,
(2)$\left\{\begin{array}{l}{a>0}\\{△={a}^{2}-4a<0}\end{array}\right.$,解得0<a<4,
所以0≤a<4,
Q真,$\frac{{x}^{2}-ax+6}{x+1}$≥2对任意的x∈N*恒成立?a≤(x+$\frac{4}{x}$-2)min=2,
所以a≤2,
∵P∧Q为假命题,P∨Q为真命题,
∴所以P与Q为一真一假,
当P真Q假时,$\left\{\begin{array}{l}{0≤a<4}\\{a>2}\end{array}\right.$,解得2<a<4,
当P假Q真时,$\left\{\begin{array}{l}{a<0或a≥4}\\{a≤2}\end{array}\right.$,解得a<0,
综上所述a的取值范围为(-∞,0)∪(2,4).
点评 本题考查命题的真假的判断与应用,考查分类讨论思想的应用,以及恒成立的问题,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
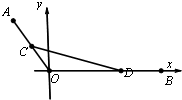 在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.
在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于任意的x∈R,x2+1≤0 | B. | 存在x∈R,x2+1≤0 | ||
| C. | 存在x∈R,x2+1<0 | D. | 存在x∈R,x2+1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{16}{9}$ | B. | $\frac{10}{9}$ | C. | $\frac{8}{9}$ | D. | $\frac{28}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
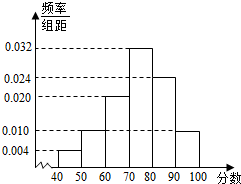 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{18}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com