
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据条件转化为求函数存在割线斜率小于1,利用导数的应用进行求解.
解答 解:对于函数f(x),在定义域内存在两个变量x1,x2且x1<x2时有f(x1)-f(x2)>x1-x2.
即等价为$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<1
即存在割线斜率小于1,
①若f(x)=ex(x>0),
则函数的导数f′(x)=ex,
∵x>0,∴f′(x)>1,不满足条件.
②若f(x)=$\frac{lnx}{x}$,则函数的导数f′(x)=$\frac{1-lnx}{{x}^{2}}$,
则当x=e时,f′(x)=$\frac{1-lne}{{e}^{2}}=0$满足f′(x)<1,即满足条件.
③若f(x)=$\sqrt{x}$,x≥0,
则则函数的导数f′(x)=$\frac{1}{2\sqrt{x}}$,
则当x=1时,f′(x)=$\frac{1}{2}$满足f′(x)<1,即满足条件.
④若f(x)=1+sinx,则f′(x)=cosx≤1,
故满足f′(x)<1,即满足条件.
故选:C
点评 本题主要考查函数的新定义,利用条件转化为斜率问题,利用导数是解决本题的关键.


科目:高中数学 来源: 题型:填空题
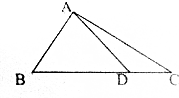 已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.
已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=sinx | B. | f(x)=-cosx | C. | f(x)=x3-x | D. | f(x)=-ex |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com