
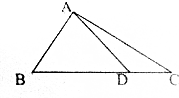
 已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1.
已知在△ABC中,点D在BC上,且满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x+y=1. 分析 由题意,利用向量的三角形法则,将$\overrightarrow{AD}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$表示,求出x,y.
解答 解:由题意,$\overrightarrow{AD}=\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{3}{4}(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{1}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}$,
所以x=$\frac{1}{4}$,y=$\frac{3}{4}$,
所以x+y=1;
故答案为:1.
点评 本题考查了向量的三角形法则的运用以及平面向量基本定理的运用;属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题“p∨q”为真命题,则命题p和命题q均为真命题 | |
| B. | am2<bm2是a<b的必要不充分条件 | |
| C. | x=2kπ+$\frac{π}{4}$(k∈Z)是(-sinx)′=(cosx)′的充要条件 | |
| D. | 命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底,则{$\overrightarrow{a}$,$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
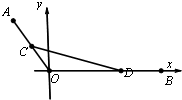 在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.
在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com