
已知空间中三点A(-2,0,2),B(-1,1, 2),C(-3,0,4),设a=
2),C(-3,0,4),设a=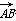 ,b=
,b=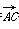 .
.
(1)若|c|=3,且c∥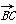 ,求向量c的坐标;
,求向量c的坐标;
(2)若m(a+b)+n(a-b)与2a-b垂直,求m,n应满足的关系式.
解:(1)由条件得a=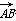 =(1,1,0),b=
=(1,1,0),b=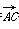 =(-1,0,2),
=(-1,0,2),
∴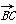 =
=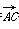 -
-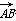 =(-2,-1,2).
=(-2,-1,2).
∵c∥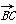 ,
,
∴c=λ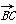 =λ(-2,-1,2)=(-2λ,-λ,2λ).
=λ(-2,-1,2)=(-2λ,-λ,2λ).
∴|c|=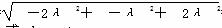 =3|λ|=3,
=3|λ|=3,
∴λ=1或λ=-1.
∴c=(-2,-1,2)或c=(2,1,-2).
(2)由条件得a+b=(0,1,2),a-b=(2,1,-2),
2a-b=(3,2,-2).
∴m(a+b)+n(a-b)=(2n,m+n,2m-2n).
∵m(a+b)+n(a-b)与2a-b垂直,
∴[m(a+b)+n(a-b)]·(2a-b)
=3·2n+2(m+n)-2(2m-2n)=12n-2m=0.
∴m=6 n.
n.
即当m=6n时,可使m(a+b)+n(a-b)与2a-b垂直.
10.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
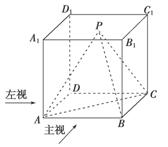
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
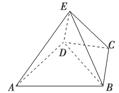
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1 及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
及其边界上运动,并且总保持AP⊥BD1,则动点P的轨迹是( )
A.线段B1C
B.线段BC1
C.BB1中点与CC1中点连成的线段
D.BC中点与B1C1中点连成的线段

查看答案和解析>>
科目:高中数学 来源: 题型:
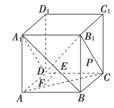
如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF,则EF与平面A1B1CD的位置关系为____ ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂生产甲、乙、丙三种型号的产品,产品数量之比为3∶5∶7,现用分层抽样的方法抽出容量为n的样本,其中甲种产品有18件,则样本容量n=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com