
| 几何题 | 代数题 | 合计 | |
| 男 | 25 | 5 | 30 |
| 女 | 10 | 10 | 20 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)利用公式K2,求出,与临界值比较,即可得出结论;
(2)X可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望E(X).
解答 解:(1)K2=$\frac{50×(25×10-10×5)^{2}}{30×20×35×15}$=$\frac{400}{63}$>5.024,故在犯错的概率不超过0.025的前提下认为视觉和空间能力与性别是有关的;…(4分)
(2)X可取的值为0,1,2,3
P(X=0)=$\frac{{C}_{7}^{3}}{{C}_{10}^{3}}$=$\frac{7}{24}$,P(X=1)=$\frac{{C}_{7}^{2}{C}_{3}^{1}}{{C}_{10}^{3}}$=$\frac{21}{40}$,
P(X=2)=$\frac{{C}_{7}^{1}{C}_{3}^{2}}{{C}_{10}^{3}}$=$\frac{7}{40}$,P(X=3)=$\frac{{C}_{3}^{3}}{{C}_{10}^{3}}$=$\frac{1}{120}$.
| X | 0 | 1 | 2 | 3 |
| P | $\frac{7}{24}$ | $\frac{21}{40}$ | $\frac{7}{40}$ | $\frac{1}{120}$ |
点评 本题考查独立性检验知识的运用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=cosx,g(x)=2 | B. | $f(x)={log_2}({{x^2}-2x+5}),g(x)=sin\frac{π}{2}x$ | ||
| C. | $f(x)=\sqrt{4-{x^2}},g(x)=\frac{3}{4}x+\frac{15}{4}$ | D. | $f(x)=x+\frac{2}{x},g(x)=lnx+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
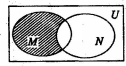 设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )
设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )| A. | {x|2≤x≤3} | B. | {x|1≤x≤2} | C. | $\{x|1≤x≤\sqrt{3}\}$ | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com