
 ��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶���ΪA�����Ҷ���ΪB��C���ҽ���ΪF��|AF|=3���ҡ�ABC���ܳ�Ϊ14��
��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����϶���ΪA�����Ҷ���ΪB��C���ҽ���ΪF��|AF|=3���ҡ�ABC���ܳ�Ϊ14������ ��1����حAFح2=b2+c2=a2����a=3��2��حACح+a��=14���������b��ֵ����c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$��������Բ�������ʹ�ʽ�����������Բ�������ʣ�
��2������һ����$\frac{|MP|}{|PN|}$=$\frac{|MQ|}{|QN|}$��������2y1y2=y0��y1+y2������ֱ�߷��̴�����Բ���̣���Τ�ﶨ�����������x0=$\frac{9}{4}$����=$\frac{حMPح}{حPNح}$=$\frac{4-{x}_{1}}{{x}_{1}-{x}_{0}}$������$\frac{9}{4}$��x1��3���������ʵ���˵�ȡֵ��Χ��
����������$\frac{|MP|}{|PN|}$=$\frac{|MQ|}{|QN|}$��������2y1y2=y0��y1+y2������ֱ�߷��̴�����Բ���̣���Τ�ﶨ�������������ʽ�����x0=$\frac{9}{4}$����=$\frac{56k}{42k\sqrt{1-{k}^{2}}}$=$\frac{4}{3\sqrt{1-{k}^{2}}}$��$\frac{4}{3}$���������ʵ���˵�ȡֵ��Χ��
�����������������$\overrightarrow{MP}$=��$\overrightarrow{PN}$��$\overrightarrow{MQ}$=-��$\overrightarrow{QN}$�������������������㣬���P��Q���꣬������Բ���̣��������x0=$\frac{9}{4}$��ͬ����һ��������ü������ʵ���˵�ȡֵ��Χ��
��� �⣺��1����حAFح2=b2+c2=a2����a=3��--------------------------��1�֣�
��ABC���ܳ�Ϊ2��حACح+a��=14����$\sqrt{{a}^{2}+{b}^{2}}$+a=7����b2=7��
��c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$��
��Բ��������Ϊe=$\frac{c}{a}$=$\frac{\sqrt{2}}{3}$��---------------------------------------------��4�֣�
��2������һ����Ȼֱ��l��б�ʴ��ڣ���l�ķ���Ϊy=k��x-4����
��P��x1��y1����Q��x2��y2����N��x0��y0����
��$\frac{|MP|}{|PN|}$=$\frac{|MQ|}{|QN|}$����$\frac{{y}_{1}}{{y}_{0}-{y}_{1}}$=$\frac{{y}_{2}}{{y}_{2}-{y}_{0}}$�������2y1y2=y0��y1+y2���٣�-----��6�֣�
��$\left\{\begin{array}{l}{y=k��x-4��}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{7}=1}\end{array}\right.$��ȥx���ã�9k2+7��y2+56ky+49k2=0��
��y1+y2=-$\frac{56k}{9{k}^{2}+7}$��y1y2=$\frac{49{k}^{2}}{9{k}^{2}+7}$��----------------------------------------------------��8�֣�
�����ʽ��y0=-$\frac{7}{4}$k����y0=k��x0-4������x0=$\frac{9}{4}$��
��=$\frac{حMPح}{حPNح}$=$\frac{4-{x}_{1}}{{x}_{1}-{x}_{0}}$=-1+$\frac{4-{x}_{0}}{{x}_{1}-{x}_{0}}$=-1+$\frac{\frac{7}{4}}{{x}_{1}-\frac{9}{4}}$��---------------------------------------��10�֣�
��$\frac{9}{4}$��x1��3����0��x1-$\frac{9}{4}$��$\frac{3}{4}$����ˡ�-1+$\frac{7}{3}$=$\frac{4}{3}$��
��ˣ�N��һ��ֱ��x=$\frac{9}{4}$�ϣ�ʵ���ˡ�[$\frac{4}{3}$��+�ޣ���------------------------------------------��12�֣�
����������Ȼֱ��l��б�ʴ��ڣ���l�ķ���Ϊy=k��x-4����������k��0��
��P��x1��y1����Q��x2��y2����N��x0��y0����y2��y1��
�ɦ�=$\frac{|MP|}{|PN|}$=$\frac{|MQ|}{|QN|}$���æ�=$\frac{{y}_{1}}{{y}_{0}-{y}_{1}}$=$\frac{{y}_{2}}{{y}_{2}-{y}_{0}}$�������2y1y2=y0��y1+y2���٣���6�֣�
��y1=�ˣ�y0-y1����y2=�ˣ�y2-y0������y1+y2=�ˣ�y2-y1�����ڣ�
��$\left\{\begin{array}{l}{y=k��x-4��}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{7}=1}\end{array}\right.$��ȥx���ã�9k2+7��y2+56ky+49k2=0��
��֪��=��56k��2-4����9k2+7����49k2=49k2-36��1-k2����0��
��y1+y2=-$\frac{56k}{9{k}^{2}+7}$��y1y2=$\frac{49{k}^{2}}{9{k}^{2}+7}$��y1��2=$\frac{-56k��\sqrt{��}}{2��9{k}^{2}+7��}$��----------------------��8�֣�
�����ʽ��y0=-$\frac{7}{4}$k����y0=k��x0-4������x0=$\frac{9}{4}$��---------------------------------------��9�֣�
�ɢ�ʽ��-$\frac{56k}{9{k}^{2}+7}$=��•$\frac{-\sqrt{��}}{9{k}^{2}+7}$���æ�=$\frac{56k}{42k\sqrt{1-{k}^{2}}}$=$\frac{4}{3\sqrt{1-{k}^{2}}}$��$\frac{4}{3}$��
��ˣ�N��һ��ֱ��x=$\frac{9}{4}$�ϣ�ʵ���ˡ�[$\frac{4}{3}$��+�ޣ���------------------------------------------��12�֣�
����������P��x1��y1����Q��x2��y2����N��x0��y0����x2��x1���ɦ�=$\frac{|MP|}{|PN|}$=$\frac{|MQ|}{|QN|}$��
��$\overrightarrow{MP}$=��$\overrightarrow{PN}$��$\overrightarrow{MQ}$=-��$\overrightarrow{QN}$��-----------------------------------------------------------------------��5�֣�
��$\left\{\begin{array}{l}{{x}_{1}=\frac{4+��{x}_{0}}{1+��}}\\{{y}_{1}=\frac{��{y}_{0}}{1+��}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{4-��{x}_{0}}{1-��}}\\{{y}_{2}=\frac{-��{y}_{0}}{1-��}}\end{array}\right.$��P��x1��y1����Q��x2��y2����������Բ���̵�------------------��7�֣�
$\left\{\begin{array}{l}{\frac{��\frac{4+��{x}_{0}}{1+��}��^{2}}{9}+\frac{��\frac{��{y}_{0}}{1+��}��^{2}}{7}=1}\\{\frac{��\frac{4-��{x}_{0}}{1-��}��^{2}}{9}+\frac{��{\frac{-��{y}_{0}}{1-��}��}^{2}}{7}=1}\end{array}\right.$��-----------------��9�֣�
������ʽ��������x0=$\frac{9}{4}$��
��=$\frac{حMPح}{حPNح}$=$\frac{4-{x}_{1}}{{x}_{1}-{x}_{0}}$=-1+$\frac{4-{x}_{0}}{{x}_{1}-{x}_{0}}$=-1+$\frac{\frac{7}{4}}{{x}_{1}-\frac{9}{4}}$��---------------------------------------��10�֣�
��$\frac{9}{4}$��x1��3����0��x1-$\frac{9}{4}$��$\frac{3}{4}$����ˡ�-1+$\frac{7}{3}$=$\frac{4}{3}$��
��ˣ�N��һ��ֱ��x=$\frac{9}{4}$�ϣ�ʵ���ˡ�[$\frac{4}{3}$��+�ޣ���----------------------------------��12�֣�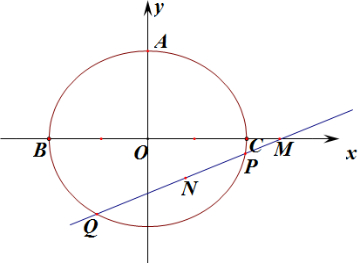
���� ���⿼����Բ�ı����̼��������ʣ�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����������������㣬������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
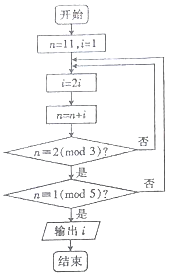 ��������N����������m�������Ϊn�����ΪN=n��mod m��������10=2��mod 4������������ͼ���㷨Դ���ҹ��Ŵ���������ġ��й�ʣ�ඨ������ִ�иó����ͼ���������i���ڣ�������
��������N����������m�������Ϊn�����ΪN=n��mod m��������10=2��mod 4������������ͼ���㷨Դ���ҹ��Ŵ���������ġ��й�ʣ�ඨ������ִ�иó����ͼ���������i���ڣ�������| A�� | 4 | B�� | 8 | C�� | 16 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
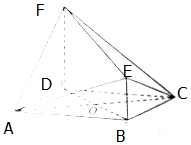 ��ͼ���ڼ�����ABCDEF�У��ı���ABCD�����Σ�BE��ƽ��ABCD��DF��BE����DF=2BE=2��EF=3��
��ͼ���ڼ�����ABCDEF�У��ı���ABCD�����Σ�BE��ƽ��ABCD��DF��BE����DF=2BE=2��EF=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0���ȣ�2��+�ޣ� | B�� | ��0��2] | C�� | [0��2] | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$ | B�� | �� | C�� | $\frac{3��}{2}$ | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{5}{18}$ | D�� | $\frac{2}{9}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com