Question

17．在△ABC中，BC=2，AC=1，以AB为边作等边三角形ABD（C，D两点在直线AB的两侧），当∠C变化时，线段CD长的最大值为3，此时C=120°．

Answer 1

分析 通过旋转三角形将长度等于CD，AC，BC的三条边转化到同一个三角形当中，使用余弦定理求出CD的最值．

解答 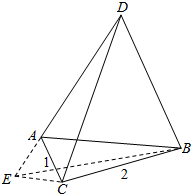解：如图，△ABD是等边三角形，将△ACD绕A逆时针旋转60°得到△AEB，
则AC=AE=1，∠CAE=60°，CD=BE，∴△ACE是等边三角形，∴CE=1，∠ACE=60°．
在△BCE中，∠BCE=∠ACB+60°，CE=1，BC=2，∴BE=$\sqrt{{2}^{2}+{1}^{2}-4cos（∠ACB+60°）}$．
∴当cos（∠ACB+60°）=-1即∠ACB=120°时BE取得最大值3．即CD的最大值是3．
故答案为3，120°．

点评 本题考查了余弦定理得应用，对三角形进行旋转，将边长为1，2，CD的线段转化到同一个三角形中是解题关键．