Question

8．如图，在四边形ABCD中，∠A=90°，AB=AD=2，CB=CD=3，将△ABD沿BD折起，得到三棱锥A'-BDC，O为BD的中点，M为OC的中点，点N在线段A'B上，满足$A'N=\frac{1}{4}A'B$．

（Ⅰ）证明：MN∥平面A'CD；
（Ⅱ）若A'C=3，求点B到平面A'CD的距离．

Answer 1

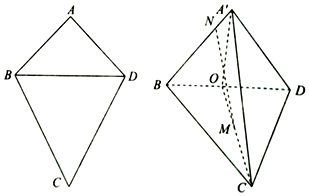
分析 （Ⅰ）过点N作BD的平行线，交直线A'D于点E，证明：四边形MNEF为平行四边形，可得MN∥EF，即可证明MN∥平面A'CD；
（Ⅱ）若A'C=3，利用等体积方法，即可求点B到平面A'CD的距离．

解答 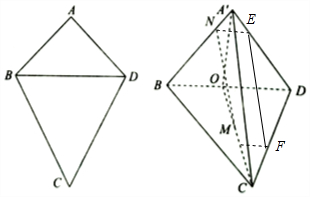（Ⅰ）证明：过点N作BD的平行线，交直线A'D于点E，
过点M作BD的平行线，交直线CD于点F，…（1分）
因为NE∥BD，MF∥BD，所以NE∥MF，
且$NE=MF=\frac{1}{4}BD$，所以四边形MNEF为平行四边形，…（3分）
所以MN∥EF，且EF?平面A'CD，MN?平面A'CD，
所以MN∥平面A'CD．…（4分）
（Ⅱ）解：因为A'C=3，所以A'O⊥OC，且A'O⊥BD，OC∩BD=O，所以A'O⊥平面BCD．…（6分）
由：V_B-A'CD=V_A'-BCD${S_{A'CD}}=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$，…（8分）
${S_{BCD}}=\frac{1}{2}×2\sqrt{2}×\sqrt{7}=\sqrt{14}$，$A'O=\sqrt{2}$，…（10分）
所求点B到平面A'CD的距离$h=\frac{{\sqrt{14}×\sqrt{2}}}{{2\sqrt{2}}}=\frac{{\sqrt{14}}}{2}$．…（12分）

点评 本题考查线面平行的判定，考查点到平面距离的计算，考查体积的计算，属于中档题．