
【题目】选修4—4:坐标系与参数方程
已知极坐标系的极点![]() 与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() ,若直线
,若直线![]() 与曲线C相交于A,B两点,且
与曲线C相交于A,B两点,且![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)若M,N为曲线C上的两点,且![]() ,求
,求![]() 的最小值.
的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点为极点,
为倾斜角),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位,曲线
轴正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和参数方程;
的普通方程和参数方程;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求线段
两点,求线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售量8万件.
(Ⅰ)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?
(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 ![]() (x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入
(x2﹣600)万元作为技改费用,投入50万元作为固定宣传费用,投入 ![]() x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log3(1+x)﹣log3(1﹣x).
(1)判断函数f(x)的奇偶性,并加以证明;
(2)已知函数g(x)=log ![]()
![]() ,当x∈[
,当x∈[ ![]() ,
, ![]() ]时,不等式 f(x)≥g(x)有解,求k的取值范围.
]时,不等式 f(x)≥g(x)有解,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}中,a2=2,a5=128.
(1)求通项an;
(2)若bn=log2an , 数列{bn}的前n项和为Sn , 且Sn=360,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 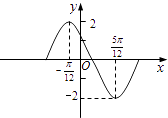
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回答下列问题
(1)已知圆C的方程为x2+y2=4,直线l过点P(1,2),且与圆C交于A、B两点.若|AB|=2 ![]() ,求直线l的方程;
,求直线l的方程;
(2)设直线l的方程为(a+1)x+y﹣2﹣a=0(a∈R).若直线l在两坐标轴上的截距相等,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com