
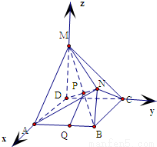
如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,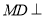 平面ABCD,
平面ABCD,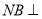 平面ABCD,且
平面ABCD,且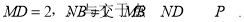
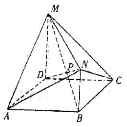
(1)在棱AB上找一点Q,使QP//平面AMD,并给出证明;
(2)求平面BNC与平面MNC所成锐二面角的余弦值.
(1)当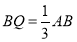 时,有
时,有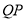 //平面AMD.
//平面AMD.
证明:因为MD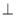 平面ABCD,NB
平面ABCD,NB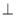 平面ABCD,所以MD//NB,
平面ABCD,所以MD//NB,
所以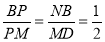 ,又
,又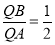 ,所以
,所以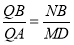 ,所以在
,所以在 中,OP//AM.
中,OP//AM.
又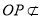 面AMD,AM
面AMD,AM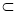 面AMD,∴
面AMD,∴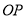 // 面AMD.
// 面AMD.
(2)锐二面角的余弦值为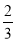 .
.
【解析】
试题分析:(1)设Q为AB上的一点,满足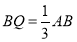 .由线面平行的性质证出MD//NB,结合题中数据利用平行线的性质,得到
.由线面平行的性质证出MD//NB,结合题中数据利用平行线的性质,得到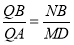 ,从而在
,从而在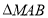 中得到OP//AM.最后利用线面平行判定定理,证出
中得到OP//AM.最后利用线面平行判定定理,证出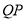 // 面AMD,说明在棱AB上存在满足条件的点;
// 面AMD,说明在棱AB上存在满足条件的点;
(2)建立如图所示空间直角坐标系,算出向量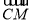 、
、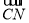 和
和 的坐标.利用垂直向量数量积为0的方法建立方程组,算出平面CMN的法向量
的坐标.利用垂直向量数量积为0的方法建立方程组,算出平面CMN的法向量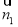 .根据线面垂直的判定定理证出DC
.根据线面垂直的判定定理证出DC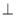 平面BNC,从而得到
平面BNC,从而得到 即是BNC的法向量,最后利用空间向量的夹角公式加以计算,即可算出平面CMN与平面BNC所成锐二面角的余弦值.
即是BNC的法向量,最后利用空间向量的夹角公式加以计算,即可算出平面CMN与平面BNC所成锐二面角的余弦值.
试题解析:(1)当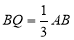 时,有
时,有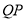 //平面AMD.
//平面AMD.
证明:因为MD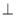 平面ABCD,NB
平面ABCD,NB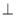 平面ABCD,所以MD//NB,
平面ABCD,所以MD//NB,
所以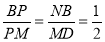 ,又
,又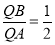 ,所以
,所以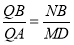 ,所以在
,所以在 中,OP//AM.
中,OP//AM.
又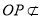 面AMD,AM
面AMD,AM 面AMD,∴
面AMD,∴ // 面AMD.
// 面AMD.
(2)以DA、DC、DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,则D(0,0,0),B(2,2,0),C(0,2,0),M(0,0,2)N(2,2,1),所以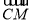 =(0,-2,2),
=(0,-2,2),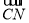 =(2,0,1),
=(2,0,1), =(0,2,0),
=(0,2,0),
设平面CMN的法向量为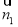 =(x,y,z)则
=(x,y,z)则 ,所以
,所以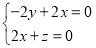 ,所以
,所以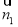 =(1,-2,-2).
=(1,-2,-2).
又NB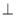 平面ABCD,∴NB
平面ABCD,∴NB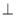 DC,BC
DC,BC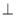 DC,∴DC
DC,∴DC 平面BNC,∴平面BNC的法向量为
平面BNC,∴平面BNC的法向量为 =
= =(0,2,0),
=(0,2,0),
设所求锐二面角为 ,则
,则 .
.
考点:利用空间向量求平面间的夹角;直线与平面平行的判定.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
| A、54 | B、56 | C、58 | D、57 |
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版) 题型:选择题
已知双曲线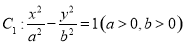 的离心率为2,若抛物线
的离心率为2,若抛物线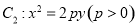 的焦点到双曲线
的焦点到双曲线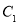 的渐近线的距离为2,则抛物线
的渐近线的距离为2,则抛物线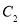 的方程为
的方程为
A.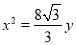 B.
B.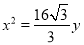 C.
C.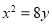 D.
D.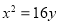
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知两个不同的平面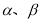 和两个不重合的直线m、n,有下列四个命题:
和两个不重合的直线m、n,有下列四个命题:
①若 ;
;
②若 ;
;
③若 ;
;
④若 .
.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
已知双曲线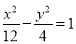 的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
A.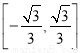 B.
B.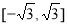 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届安徽省皖南八校高三第一次联考文科数学试卷(解析版) 题型:选择题
已知函数 ,若f(x)存在唯一的零点
,若f(x)存在唯一的零点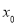 ,且
,且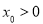 ,则a的取值范围是( )
,则a的取值范围是( )
A.(2,+∞) B.(一∞,-2) C.(1,+∞) D.(一∞,一1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com