
分析 (1)求出函数的导数,计算f′(1),f(1)求出a,b的值,求出函数的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间和最值即可;
(2)令g(x)=x-sinx,x>0,得到当x>0时,x>sinx,令h(x)=ex-x-1,x>0,根据函数的单调性将问题转化为只需证$x+1+lnx>2-\frac{1}{x}$,根据函数的单调性证明即可.
解答 解:(1)f'(x)=1+lnx+a,
故f'(1)=1+a=1,得a=0,又2-2f(1)-1=0,
所以$f(1)=a+b=\frac{1}{2}$,得$b=\frac{1}{2}$.
则$f(x)=xlnx+\frac{1}{2}$,f'(x)=1+lnx,
当$x∈({0,\frac{1}{e}}]$时,f'(x)≤0,f(x)单调递减;
当$x∈({\frac{1}{e},+∞})$时,f'(x)>0,f(x)单调递增,
所以$f{({\frac{1}{e}})_{min}}=\frac{1}{2}-\frac{1}{e}$.
(2)证明:令g(x)=x-sinx,x>0,g'(x)=1-cosx≥0,g(x)递增,
所以g(x)>g(0)=0,所以当x>0时,x>sinx,
令h(x)=ex-x-1,x>0,h'(x)=ex-1≥0,h(x)递增,
h(x)>h(0)=0,所以当x>0时,ex>x+1,
要证${e^x}+lnx>cosx+\frac{sinx-1}{x}$,由-1≤cosx≤1,x>sinx,及ex>x+1,
得,${e^x}+lnx>x+1+lnx,cosx+\frac{sinx-1}{x}<1+1-\frac{1}{x}$,故原不等式成立,
只需证$x+1+lnx>2-\frac{1}{x}$,
即证x2-x+1+xlnx>0.由(1)可得$xlnx≥-\frac{1}{e}$,且${x^2}-x+1≥\frac{3}{4}$,
所以${x^2}-x+1+xlnx>\frac{3}{4}-\frac{1}{e}>0$,则原不等式成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查不等式的证明,是一道综合题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
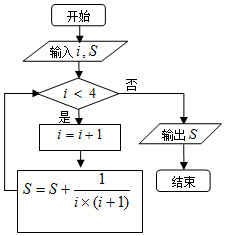
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A类 | B类 | C类 | |
| 男生 | 18 | x | 3 |
| 女生 | 10 | 8 | y |
| 男生 | 女生 | 总计 | |
| A类 | |||
| B类和C类 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,5} | B. | {3,4,5} | C. | {x|3≤x<4} | D. | {x|3≤x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | $\frac{y^2}{3}-{x^2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | ${y^2}-\frac{x^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
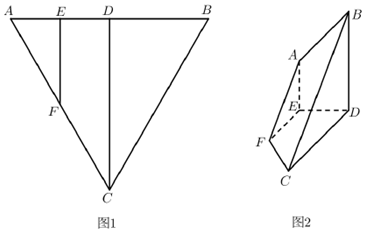
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
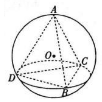 体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )
体积为$18\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是( )| A. | [4π,12π] | B. | [8π,16π] | C. | [8π,12π] | D. | [12π,16π] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com