Question

12．对a、b∈R，记$max\left\{{a\;，\;\;b}\right\}=\left\{\begin{array}{l}a\;，\;\;a≥b\\ b\;，\;\;a＜b\end{array}\right.$，函数f（x）=max{|x|，-x²-2x+2}，x∈（-4，3）
（1）求f（0），f（-3）；
（2）写出解析式，并作出f（x）的图象；
（3）就k的值讨论关于x的议程f（x）=k解的个数情况．

Answer 1

分析 （1）分别求出f（0），f（-3）比较即可，
（2）写出函数的解析式，并画出图象，
（2）结合图象分类讨论即可．

解答 解：（1）∵f（0）=|0|=0，或f（0）=-0-0+2=2，
∴f（0）=2，
∵f（-3）=|-3|=3，或f（-3）=-9+6+2=-1，
∴f（-3）=3，
（2）由题意可得f（x）=$\left\{\begin{array}{l}{|x|，-4＜x≤-2，或\frac{-3+\sqrt{17}}{2}≤x＜3}\\{-{x}^{2}-2x+2，-2＜x＜\frac{-3+\sqrt{17}}{2}}\end{array}\right.$，其图象如图所示，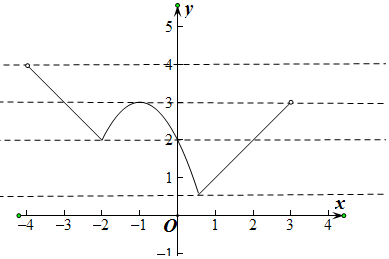

由图象可知，
当k≥4或k＜$\frac{-3+\sqrt{17}}{2}$时，
方程f（x）=k无解，
当3＜k＜4，或k=$\frac{-3+\sqrt{17}}{2}$时，
方程f（x）=k有唯一解，
当2＜k＜3时，方程f（x）=k有四个解，
当k=2时，方程f（x）=k有三个解，
当$\frac{-3+\sqrt{17}}{2}$＜k＜2时，方程f（x）=k有两个解．

点评 本题考查了新定义的应用，以及分段函数的问题，关键是画图，属于中档题．