
 如图,已知F为抛物线y2=4x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.
如图,已知F为抛物线y2=4x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F.分析 (Ⅰ)设A(x1,y1),B(x2,y2),C(x1,-y1),运用三角形的重心坐标公式和抛物线方程,即可求得A,B的坐标,进而得到直线方程;
(Ⅱ)通过直线BC,AB的方程和抛物线方程,运用韦达定理,可得恒过定点(-1,0),即有S△ABO=$\frac{1}{2}$|OE|•|y2-y1|=$\frac{1}{2}$|y2-y1|,S△CFO=$\frac{1}{2}$|OF|•|y1|=$\frac{1}{2}$|y1|,y1y2=4,再由基本不等式计算即可得到最小值.
解答 解:(Ⅰ)设A(x1,y1),B(x2,y2),C(x1,-y1),
则△ABC的重心坐标为G($\frac{2{x}_{1}+{x}_{2}}{3}$,$\frac{{y}_{2}}{3}$),
由题意可得2x1+x2=$\frac{9}{2}$,且y2=4,
由y22=4x2,y12=4x1,
可得x2=4,y2=4,和x1=$\frac{1}{4}$,y1=1,
直线AB的斜率k=$\frac{4-1}{4-\frac{1}{4}}$=$\frac{4}{5}$,
即有直线AB的方程为4x-5y+4=0;
(Ⅱ)设A(x1,y1),B(x2,y2),C(x1,-y1),
设直线BC:x=my+1,代入抛物线方程y2=4x,可得
y2-4my-4=0,可得-y1y2=-4,即y1y2=4,
再设直线AB:y=kx+n,代入抛物线方程,可得
ky2-4y+4n=0,y1y2=$\frac{4n}{k}$=4,即n=k,
则有直线AB:y=k(x+1),即有直线AB恒过定点E(-1,0),
则S△ABO=$\frac{1}{2}$|OE|•|y2-y1|=$\frac{1}{2}$|y2-y1|,
S△CFO=$\frac{1}{2}$|OF|•|y1|=$\frac{1}{2}$|y1|,
即有S12+S22=$\frac{1}{4}$(y2-y1)2+$\frac{1}{4}$y12=$\frac{2{{y}_{1}}^{2}+{{y}_{2}}^{2}-8}{4}$=$\frac{1}{4}$(2y12+$\frac{16}{{{y}_{1}}^{2}}$-8)
≥$\frac{1}{4}$(2$\sqrt{2{{y}_{1}}^{2}•\frac{16}{{{y}_{1}}^{2}}}$-8)=2$\sqrt{2}$-2.
即有S12+S22的最小值为2$\sqrt{2}$-2,当且仅当y1=${2}^{\frac{3}{4}}$,y2=${2}^{\frac{5}{4}}$.
点评 本题考查抛物线的方程和性质,主要考查联立直线方程和抛物线的方程,运用韦达定理,同时考查基本不等式的运用:求最值,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围为[-$\sqrt{2}$,$\sqrt{2}$].
如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围为[-$\sqrt{2}$,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=ln(x+1) | C. | y=($\frac{1}{2}$)x | D. | y=x+$\frac{1}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=CD=1,AB∥CD,顶点D1在底面ABCD内的射影恰为点C.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB=2,BC=CD=1,AB∥CD,顶点D1在底面ABCD内的射影恰为点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
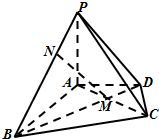 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x<0,使得2x≥1 | B. | 任意x<0,都有2x<1 | ||
| C. | 存在x<0,使得AF∥平面BCE | D. | 存在x≥0,使得2x<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com