Question

4．将边长为2的等边△PAB沿x轴正方向滚动，某时刻P与坐标原点重合（如图），设顶点P（x，y）的轨迹方程是y=f（x），关于函数y=f（x）的有下列说法：
①f（x）的值域为[0，2]；
②f（x）是周期函数；
③f（4.1）＜f（π）＜f（2014）；
④${∫}_{0}^{6}$f（x）dx=$\frac{9π}{2}$．
其中正确的个数是（　　）

• A． 0
• B． 1
• C． 2
• D． 3

Answer 1

分析 先根据题意画出顶点P（x，y）的轨迹，如图所示．轨迹是一段一段的圆弧组成的图形．从图形中可以看出，关于函数y=f（x）的说法的正确性．

解答 解：根据题意画出顶点P（x，y）的轨迹，如图所示．轨迹是一段一段的圆弧组成的图形．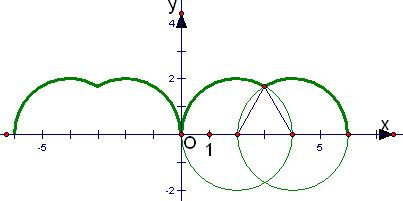

从图形中可以看出，关于函数y=f（x）的有下列说法：
①f（x）的值域为[0，2]，正确；
②f（x）是周期函数，周期为6，②正确；
③由于f（4.1）=f（3.9），f（2014）=f（4）；
f（x）在[3，4]上为增函数，
而f（π）＜f（3.9）＜f（4），
∴f（π）＜f（4.1）＜f（2014）；故③不正确；
④${∫}_{0}^{6}$f（x）dx表示函数f（x）在区间[0，6]上与x轴所围成的图形的面积，其大小为一个正三角形和二段扇形的面积和，
其值为2×$\frac{1}{3}$×2²×π+$\frac{\sqrt{3}}{4}$×2²=$\frac{8π}{3}$+$\sqrt{3}$，故④错误．
故正确的个数有2个，
故选：C

点评 本小题主要考查命题的真假判断与应用、函数单调性的应用、函数奇偶性的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．