
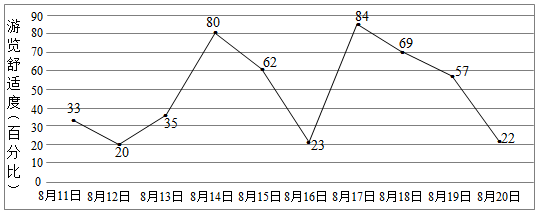
分析 设Ai表示事件“小明8月11日起第i日连续两天游览主题公园”(i=1,2,…,9).根据题意,$P({A_i})=\frac{1}{9}$,且事件Ai与Aj互斥.
(Ⅰ)设B为事件“小明连续两天都遇上拥挤”,则B=A4∪A7.利用互斥事件的概率计算公式即可得出.
(Ⅱ)由题意,可知X的所有可能取值为0,1,2,结合图象,利用互斥事件与古典概率计算公式即可得出.
(Ⅲ)从8月16日开始连续三天游览舒适度的方差最大.
解答 解:设Ai表示事件“小明8月11日起第i日连续两天游览主题公园”(i=1,2,…,9).
根据题意,$P({A_i})=\frac{1}{9}$,且事件Ai与Aj互斥.…(1分)
(Ⅰ)设B为事件“小明连续两天都遇上拥挤”,
则B=A4∪A7.…(2分)
所以$P(B)=P({A_4}∪{A_7})=P({A_4})+P({A_7})=\frac{2}{9}$.…(5分)
(Ⅱ)由题意,可知X的所有可能取值为0,1,2,…(6分)
$P(X=0)=P({A_4}∪{A_7}∪{A_8})=P({A_4})+P({A_7})+P({A_8})=\frac{1}{3}$,…(7分)
$P(X=1)=P({A_3}∪{A_5}∪{A_6}∪{A_9})=P({A_3})+P({A_5})+P({A_6})+P({A_9})=\frac{4}{9}$,…(8分)
$P(X=2)=P({A_1}∪{A_2})=P({A_1})+P({A_2})=\frac{2}{9}$. …(9分)
所以X的分布列为
| X | 0 | 1 | 2 |
| P | $\frac{1}{3}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
点评 本题考查了随机变量的分布列及其数学期望、互斥事件与古典概率计算公式、数形结合思想方法,考查了推理能力与计算能力,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
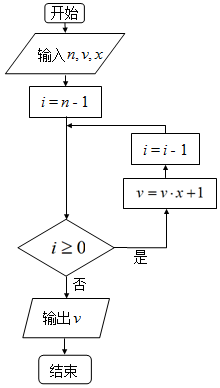 我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )
我国南宋时期的数学家秦九韶(约1202-1261)在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,v=1,x=2,则程序框图计算的是( )| A. | 25+24+23+22+2+1 | B. | 25+24+23+22+2+5 | ||
| C. | 26+25+24+23+22+2+1 | D. | 24+23+22+2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
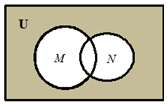 已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )
已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )| A. | {x|x<2} | B. | {x|1<x<2} | C. | {x|x>3} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
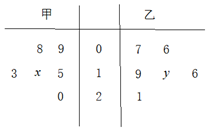 如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.
如图茎叶图记录了甲,乙两班各六名同学一周的课外阅读时间(单位:小时),已知甲班数据的平均数为13,乙班数据的中位数为17,那么x的位置应填3;y的位置应填8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com