
分析 运用向量数量积的定义和余弦定理,解方程可得BC的长.
解答 解:由AB=4,AC=3,$\overrightarrow{AC}$•$\overrightarrow{BC}$=1,
可得|$\overrightarrow{AC}$|•|$\overrightarrow{BC}$|cosC=3|$\overrightarrow{BC}$|•$\frac{|\overrightarrow{AC}{|}^{2}+|\overrightarrow{BC}{|}^{2}-|\overrightarrow{AB}{|}^{2}}{2|\overrightarrow{AC}|•|\overrightarrow{BC}|}$=1,
即有2|$\overrightarrow{AC}$|=3(|$\overrightarrow{AC}$|2+|$\overrightarrow{BC}$|2-|$\overrightarrow{AB}$|2),
即为6=3(9+|$\overrightarrow{BC}$|2-16),
解得|$\overrightarrow{BC}$|=3,
故答案为:3.
点评 本题考查向量数量积的定义和解三角形的余弦定理的运用,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
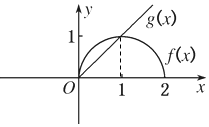 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与第几次抽样无关,每次抽中的可能性相等 | |
| B. | 与第几次抽样无关,第一次抽中的可能性要大些 | |
| C. | 与第几次抽样有关,最后一次抽中的可能性大些 | |
| D. | 与第几次抽样有关,虽然每次都是等可能的抽取,但各次抽取的可能性不一样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1,a100 | B. | a100,a44 | C. | a45,a44 | D. | a44,a45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com