
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.证明:直线
的中点.证明:直线![]() 平面
平面![]() .
.

【答案】证明见解析
【解析】
试题方法一,取OB的中点G,连接GN、GM。证明平面MNG∥平面OCD,从而可证得MN∥平面OCD。
方法二:取OD的中点P,连接MP、CP。可证得四边形MNCP为平行四边形,因此MN∥PC,由线面平行的判定定理可得MN∥平面OCD。
试题解析:
方法一:如图,取OB的中点G,连接GN、GM。
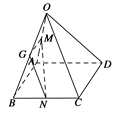
∵M为OA的中点,
∴MG∥AB.
∵AB∥CD,
∴MG∥CD.
∵MG![]() 平面OCD,CD平面OCD,
平面OCD,CD平面OCD,
∴MG∥平面OCD。
又G、N分别为OB、BC的中点,
∴GN∥OC。
∵GN![]() 平面OCD,OC平面OCD,
平面OCD,OC平面OCD,
∴GN∥平面OCD。
又MG∩GN=G,
∴平面MNG∥平面OCD。
∵MN平面MNG,
∴MN∥平面OCD。
方法二:如图,取OD的中点P,连接MP、CP。
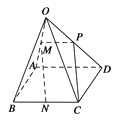
∵M为OA的中点,
∴![]() 且
且![]() 。
。
∵N为BC的中点,
∴![]() 且
且![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形MNCP为平行四边形,
∴MN∥PC。
又∵MN![]() 平面OCD,PC平面OCD,
平面OCD,PC平面OCD,
∴MN∥平面OCD.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 的图像与
的图像与![]() 轴的交点为
轴的交点为![]() ,在
,在![]() 轴右侧的第一个最高点和第一个与
轴右侧的第一个最高点和第一个与![]() 轴交点分别为
轴交点分别为![]()
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 图像上所有点的横坐标变为原来的
图像上所有点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图像沿
倍(纵坐标不变),再将所得图像沿![]() 轴正方向平移
轴正方向平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像,求
的图像,求![]() 的解析式;
的解析式;
(3)在(2)的条件下求函数![]() 在
在![]() 上的值域。
上的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+c满足f'(0)=4,f'(-2)=0。
(1)求a,b的值及曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若函数f(x)有三个不同的零点,求c的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
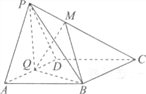
(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB;
(Ⅲ)在(Ⅱ)的条件下,若平面PAD⊥平面ABCD,且PA=PD=AD=2,求二面角M-BQ-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC为锐角三角形,命题p:不等式logcosC ![]() >0恒成立,命题q:不等式logcosC
>0恒成立,命题q:不等式logcosC ![]() >0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
>0恒成立,则复合命题p∨q、p∧q、¬p中,真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司有7辆可载![]() 的
的![]() 型卡车与4辆可载
型卡车与4辆可载![]() 的
的![]() 型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运
型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运![]() 沥青的任务,已知每辆卡车每天往返的次数为
沥青的任务,已知每辆卡车每天往返的次数为![]() 型车8次,
型车8次, ![]() 型车6次,每辆卡车每天往返的成本费为
型车6次,每辆卡车每天往返的成本费为![]() 型车160元,
型车160元, ![]() 型车252元,每天派出
型车252元,每天派出![]() 型车和
型车和![]() 型车各多少辆,公司所花的成本费最低?
型车各多少辆,公司所花的成本费最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
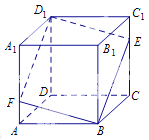
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】常州地铁项目正在紧张建设中,通车后将给市民出行带来便利.已知某条线路通车后,地铁的发车时间间隔 ![]() (单位:分钟)满足
(单位:分钟)满足![]() ,
,![]() .经测算,地铁载客量与发车时间间隔
.经测算,地铁载客量与发车时间间隔![]() 相关,当
相关,当![]() 时地铁为满载状态,载客量为1200人,当
时地铁为满载状态,载客量为1200人,当![]() 时,载客量会减少,减少的人数与
时,载客量会减少,减少的人数与![]() 的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为
的平方成正比,且发车时间间隔为2分钟时的载客量为560人,记地铁载客量为![]() .
.
⑴ 求![]() 的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
的表达式,并求当发车时间间隔为6分钟时,地铁的载客量;
⑵ 若该线路每分钟的净收益为![]() (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
(元),问当发车时间间隔为多少时,该线路每分钟的净收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com