
分析 根据同角三角函数关系式求值即可.
解答 解:(1)由sin(x+π)+cos(x-π)=$\frac{1}{2}$,
可得:-sinx-cosx=$\frac{1}{2}$,即sinx+cosx=$-\frac{1}{2}$,
那么:(sinx+cosx)2=$\frac{1}{4}$,
得:2sinxcosx=-$\frac{3}{4}$
∴sinxcosx=$-\frac{3}{8}$;
(2)∵x∈(0,π).
sinx+cosx=$-\frac{1}{2}$
∴cosx<0,sinx>0
∴sinx-cosx>0
则(sinx-cosx)2=(sinx+cosx)2-4sinxcosx=$\frac{1}{4}$-4×($-\frac{3}{8}$)=$\frac{7}{4}$
∴sinx-cosx=$\frac{{\sqrt{7}}}{2}$.
点评 本题主要考察了同角三角函数关系式的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
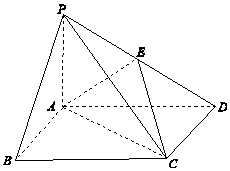 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
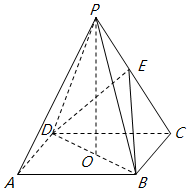 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k) | … | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | … |
| k | … | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | … |
| A. | 90% | B. | 95% | C. | 97.5% | D. | 99.5% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | m=-1 | C. | m>-1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
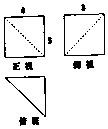 某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.
某几何体的三视图(单位:cm)如图所示,则此几何体的所有棱长之和为27+$\sqrt{34}$+$\sqrt{41}$cm,体积为20cm3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com