
 已知△ABC是等边三角形,AB=AC=BC=3,点D,E分别是边AB,AC上的点,且满足$\frac{AD}{DB}$=$\frac{CE}{EA}$=$\frac{1}{2}$,将△ADE沿DE折起到△A1DE的位置,并使得平面A1DE⊥平面BCED
已知△ABC是等边三角形,AB=AC=BC=3,点D,E分别是边AB,AC上的点,且满足$\frac{AD}{DB}$=$\frac{CE}{EA}$=$\frac{1}{2}$,将△ADE沿DE折起到△A1DE的位置,并使得平面A1DE⊥平面BCED分析 (Ⅰ)等边△ABC的边长为3,且满足$\frac{AD}{DB}$=$\frac{CE}{EA}$=$\frac{1}{2}$,求得AD和AE的值.进而由余弦定理得DE,根据AD2+DE2=AE2,判断AD⊥DE折叠后A1D⊥DE,根据平面A1DE⊥平面BCED,又利用面面垂直的性质定理推断出A1D⊥平面BCED,进而可知A1D⊥EC.
(Ⅱ)作EH⊥DC于H,则EH?平面CED,平面A1DC∩平面CED=DC,可得EH⊥平面A1DC
又作DG⊥AG于G,在△DEC中,$\frac{1}{2}DC•EH=\frac{1}{2}EC•DG$,$EH=\frac{\sqrt{21}}{14}$,即点E到平面A1DC的距离为$\frac{\sqrt{21}}{14}$.
解答 证明:(Ⅰ)因为等边△ABC的边长为3,且满足$\frac{AD}{DB}$=$\frac{CE}{EA}$=$\frac{1}{2}$,
所以AD=1,AE=2.在△ADE中,∠DAE=60°,
由余弦定理得DE=$\sqrt{{1}^{2}+{2}^{2}-2×1×2×cos6{0}^{0}}=\sqrt{3}$
因为AD2+DE2=AE2,所以AD⊥DE.折叠后有A1D⊥DE,
因为平面A1DE⊥平面BCED,又平面A1DE∩平面BCED=DE,
A1D?平面A1DE,A1D⊥DE,所以A1D⊥平面BCED
故A1D⊥EC.
解:(Ⅱ)由(Ⅰ)知DE=$\sqrt{3}$,∠DEA=30°,A1D⊥平面BCED,
则∠DEC=150°,平面A1DC⊥平面CED,
作EH⊥DC于H,则EH?平面CED,平面A1DC∩平面CED=DC,
∴EH⊥平面A1DC,
又DC=$\sqrt{D{E}^{2}+E{C}^{2}-2DE•EC•cos∠DEC}$=$\sqrt{7}$,
又作DG⊥AG于G,则DG=$\frac{\sqrt{3}}{2}$,
又在△DEC中,$\frac{1}{2}DC•EH=\frac{1}{2}EC•DG$,∴$EH=\frac{\sqrt{21}}{14}$
∴点E到平面A1DC的距离为$\frac{\sqrt{21}}{14}$.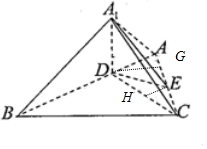
点评 本题考查了线线垂直的判定,几何法求点面距离,属于中档题,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | EX=$\frac{10}{3}$,DX=$\frac{20}{3}$ | B. | EX=$\frac{20}{3}$,DX=$\frac{10}{3}$ | C. | EX=$\frac{10}{3}$,DX=$\frac{20}{9}$ | D. | EX=$\frac{20}{3}$,DX=$\frac{20}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 样本容量为200的频率分布直方图如图所示,根据样本的频率分布直方图估计,总体数据落在[2,10)内的概率约为( )
样本容量为200的频率分布直方图如图所示,根据样本的频率分布直方图估计,总体数据落在[2,10)内的概率约为( )| A. | 0.2 | B. | 0.4 | C. | 0.8 | D. | 0.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{64}$ | B. | $\frac{3}{64}$ | C. | $\frac{27}{64}$ | D. | $\frac{9}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com