
| A. | $\frac{16}{3}$π | B. | 16π | C. | $\frac{64}{3}$π | D. | 64π |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60π | B. | 30π | C. | 20π | D. | 15π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
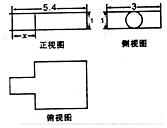 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )| A. | 2.4 | B. | 1.8 | C. | 1.6 | D. | 1.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com