
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .当
.当![]() 轴时,
轴时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知条件得b2=a2﹣1,利用通径公式得出|AB|的表达式,再由△ABM的面积得出有关a的方程,求出a的值,可得出椭圆C的标准方程;
(2)对直线l与x轴垂直、与y轴垂直以及与斜率存在且不为零三种情况讨论.在前两种情况下可直接进行验证;在第三种情况下,设直线l的方程为y=k(x﹣1)(k≠0),将直线l的方程与椭圆方程联立,列出韦达定理,利用斜率公式并代入韦达定理,通过化简计算得出结论成立.
(1)依题意得![]() ,即
,即![]() ,
,
所以当![]() 时,解得
时,解得![]() ,当
,当![]() 轴时,
轴时,![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)当![]() 与
与![]() 轴重合时,
轴重合时,![]() ,满足条件;当
,满足条件;当![]() 与
与![]() 轴垂直时,满足条件,
轴垂直时,满足条件,
当![]() 与
与![]() 轴不重合且不垂直时,设
轴不重合且不垂直时,设![]() 为
为![]() ,
,![]() ,
,![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
则![]() ,
,![]() ,
,
因为![]()
![]() ,
,
而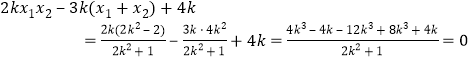 ,
,
所以![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:  ,其中
,其中![]() 是仪器的月产量.(注:总收益=总成本+利润)
是仪器的月产量.(注:总收益=总成本+利润)
(1)将利润![]() 表示为月产量
表示为月产量![]() 的函数;
的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司订购了一批树苗,为了检测这批树苗是否合格,从中随机抽测![]() 株树苗的高度,经数据处理得到如图的频率分布直方图,起中最高的
株树苗的高度,经数据处理得到如图的频率分布直方图,起中最高的![]() 株树苗高度的茎叶图如图所示,以这
株树苗高度的茎叶图如图所示,以这![]() 株树苗的高度的频率估计整批树苗高度的概率.
株树苗的高度的频率估计整批树苗高度的概率.

(1)求这批树苗的高度高于![]() 米的概率,并求图19-1中,
米的概率,并求图19-1中,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批树苗中随机选取![]() 株,记
株,记![]() 为高度在
为高度在![]() 的树苗数列,求
的树苗数列,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)若变量![]() 满足
满足![]() 且
且 ![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批树苗的高度满足近似于正态分布
的概率分布.如果这批树苗的高度满足近似于正态分布![]() 的概率分布,则认为这批树苗是合格的,将顺利获得签收;否则,公司将拒绝签收.试问,该批树苗能否被签收?
的概率分布,则认为这批树苗是合格的,将顺利获得签收;否则,公司将拒绝签收.试问,该批树苗能否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象如图,
图象如图,![]() 是
是![]() 的导函数,则下列数值排序正确的是( )
的导函数,则下列数值排序正确的是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
【答案】C
【解析】结合函数的图像可知过点![]() 的切线的倾斜角最大,过点
的切线的倾斜角最大,过点![]() 的切线的倾斜角最小,又因为点
的切线的倾斜角最小,又因为点![]() 的切线的斜率
的切线的斜率![]() ,点
,点![]() 的切线斜率
的切线斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,故
,故![]() ,应选答案C。
,应选答案C。
点睛:本题旨在考查导数的几何意义与函数的单调性等基础知识的综合运用。求解时充分借助题设中所提供的函数图形的直观,数形结合进行解答。先将经过两切点![]() 的直线绕点
的直线绕点![]() 逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点
逆时针旋转到与函数的图像相切,再将经过两切点的直线绕点![]() 顺时针旋转到与函数的图像相切,这个过程很容易发现
顺时针旋转到与函数的图像相切,这个过程很容易发现![]() ,从而将问题化为直观图形的问题来求解。
,从而将问题化为直观图形的问题来求解。
【题型】单选题
【结束】
9
【题目】已知![]() 、
、![]() 为双曲线
为双曲线![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 在
在![]() 上,
上,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,数列
为实数,数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)当![]() 和
和![]() 时,分别写出数列
时,分别写出数列![]() 的前5项;
的前5项;
(Ⅱ)证明:当![]() 时,存在正整数
时,存在正整数![]() ,使得
,使得![]() ;
;
(Ⅲ)当![]() 时,是否存在实数
时,是否存在实数![]() 及正整数
及正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ?若存在,求出实数
?若存在,求出实数![]() 及正整数
及正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com