
| A. | |$\overrightarrow{b}$|=1 | B. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$•$\overrightarrow{b}$=1 | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$ |
分析 由已知可得$\overrightarrow{b}=\frac{1}{2}\overrightarrow{BC}$,然后逐一验证四个选项得答案.
解答 解:∵△ABC是边长为2的等边三角形,且$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{a}$+2$\overrightarrow{b}$,
∴$2\overrightarrow{b}=\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}$,则$|\overrightarrow{b}|=\frac{1}{2}|\overrightarrow{BC}|=1$,A正确;
∵($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{b}$=$\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}=\overrightarrow{AB}•\frac{1}{2}\overrightarrow{BC}+1$=$\frac{1}{2}×2×2×cos120°+1=0$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,故B正确;
$\overrightarrow{a}•\overrightarrow{b}=0-|\overrightarrow{b}{|}^{2}=-1$,故C错误;
$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}=\sqrt{|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}}$
=$\sqrt{4+2×2×1×cos120°+1}$=$\sqrt{3}$,故D正确.
故选:C.
点评 本题考查平面向量的数量积运算,考查了数学转化思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m、n都平行于平面α,则m、n一定不是相交直线 | |
| B. | 若m、n都垂直于平面α,则m、n一定是平行直线 | |
| C. | 已知α、β互相平行,m、n互相平行,若m∥α,则n∥β | |
| D. | 若m、n在平面α内的射影互相平行,则m、n互相平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={({\frac{1}{2}})^x}$ | B. | $y=\frac{2}{x}$ | C. | y=-2x3 | D. | $y={log_2}{x^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
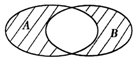 设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )
设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )| A. | [-1,0] | B. | (-1,0) | C. | (-∞,-1)∪[0,1) | D. | (-∞,-1]∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 99 | C. | 120 | D. | 121 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com