
分析 (Ⅰ)通过递推关系式直接求出a1,利用Sn+an=4,Sn-1+an-1=4,两式相减得,2an=an-1,说明数列{an}是以2为首项,公比为$\frac{1}{2}$的等比数列,求出通项公式.
(Ⅱ)化简cn=log2an-bn=19-3n,判断数列{cn}是等差数列,且公差d<0,{cn}的前n项和Tn最大值是它的所有正项数之和,求解即可.
解答 解:(Ⅰ)a1+a1=4,所以a1=2…(1分)
由Sn+an=4得n≥2时,Sn-1+an-1=4…(2分)
两式相减得,2an=an-1,$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}$,…(3分)
数列{an}是以2为首项,公比为$\frac{1}{2}$的等比数列,
所以${a_n}={2^{2-n}}$(n∈N*)…(5分)
(Ⅱ)由题,cn=log2an-bn=19-3n…(6分)
在{cn}中,cn-cn-1=-3,所以数列{cn}是等差数列,且公差d<0…(7分)
所以{cn}的前n项和Tn最大值是它的所有正项数之和.…(9分)
${c_n}≥0,即19-3n≥0,得n≤\frac{19}{3}$…(10分)
所以n=6时取得最大值.…(11分)
即(Sn)max=S6=51…(12分)
点评 本题考查递推关系式的应用,数列求和以及等差数列等比数列的判断,考查计算能力.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
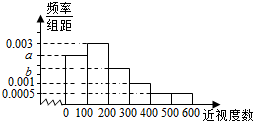 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 270 | B. | 273 | C. | 276 | D. | 279 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com