
若数列 满足①
满足① ,②存在常数
,②存在常数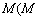 与
与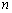 无关),使
无关),使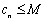 .则称数列
.则称数列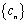 是“和谐数列”.
是“和谐数列”.
(1)设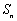 为等比数列
为等比数列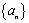 的前
的前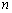 项和,且
项和,且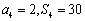 ,求证:数列
,求证:数列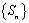 是“和谐数列”;
是“和谐数列”;
(2)设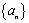 是各项为正数,公比为q的等比数列,
是各项为正数,公比为q的等比数列,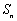 是
是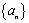 的前
的前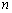 项和,求证:数列
项和,求证:数列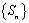 是“和谐数列”的充要条件为
是“和谐数列”的充要条件为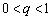 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
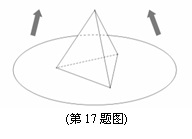
某商场为促销要准备一些正三棱锥形状的装饰品,用半径为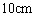 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为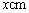 ,体积为
,体积为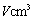 .
.
(1)求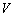 关于
关于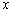 的函数关系式;
的函数关系式;
(2)在所有能用这种包装纸包装的正三棱锥装饰品中,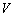 的最大值是多少?并求此时
的最大值是多少?并求此时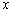 的
的
值.
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙三位同学商量高考后外出旅游,甲提议去古都西安,乙提议去海上花园厦门,丙表示随意.最终,三人商定以抛硬币的方式决定结果.规则是:由丙抛掷硬币若干次,若正面朝上,则甲得一分、乙得零分;若反面朝上,则乙得一分、甲得零分,先得4分者获胜.三人均执行胜者的提议.若记所需抛掷硬币的次数为X.
(1)求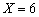 的概率;
的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点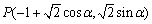 (其中
(其中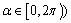 ,点
,点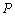 的轨迹记为曲线
的轨迹记为曲线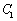 ,以坐标原点为极点,
,以坐标原点为极点,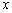 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点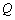 在曲线
在曲线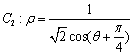 上.
上.
(Ⅰ)求曲线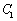 的极坐标方程和曲线
的极坐标方程和曲线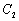 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当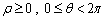 时,求曲线
时,求曲线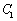 与曲线
与曲线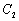 的公共点的极坐标.
的公共点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com