
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
科目:高中数学 来源: 题型:选择题
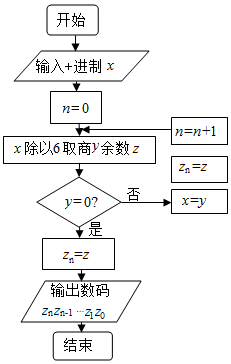 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )| A. | 682 | B. | 683 | C. | 692 | D. | 693 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 1 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
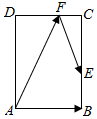 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,点E在边BC上,点F在边CD上,若$\overrightarrow{DF}$=λ$\overrightarrow{DC}$,$\overrightarrow{CE}$=λ2$\overrightarrow{CB}$,则$\overrightarrow{AF}$•$\overrightarrow{FE}$的最大值为$\frac{1}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
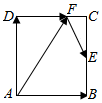 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com