
| A. | -$\frac{2015}{2016}$ | B. | -$\frac{2016}{2015}$ | C. | -$\frac{2017}{2016}$ | D. | -$\frac{2016}{2017}$ |
分析 由2Sn=an2+an(n∈N*),an>0,可得:当n=1时,$2{a}_{1}={a}_{1}^{2}$+a1,解得a1.当n≥2时,化为:(an+an-1)(an-an-1-1)=0,可得an-an-1=1,利用等差数列的通项公式及其前n项和公式可得:an,Sn.可得cn=(-1)n$•\frac{2n+1}{n(n+1)}$=(-1)n$(\frac{1}{n}+\frac{1}{n+1})$,即可得出.
解答 解:∵2Sn=an2+an(n∈N*),an>0,∴当n=1时,$2{a}_{1}={a}_{1}^{2}$+a1,解得a1=1.
当n≥2时,2an=2(Sn-Sn-1)=an2+an-$({a}_{n-1}^{2}+{a}_{n-1})$,化为:(an+an-1)(an-an-1-1)=0,
∴an-an-1=1,
∴数列{an}是等差数列,公差为1,首项为1.
∴an=1+(n-1)=n.
Sn=$\frac{n(n+1)}{2}$.
∴cn=(-1)n$\frac{2{a}_{n}+1}{2{S}_{n}}$=(-1)n$•\frac{2n+1}{n(n+1)}$=(-1)n$(\frac{1}{n}+\frac{1}{n+1})$,
则数列{cn}的前2016项的和=-$(1+\frac{1}{2})$+$(\frac{1}{2}+\frac{1}{3})$-$(\frac{1}{3}+\frac{1}{4})$+…+$(\frac{1}{2016}+\frac{1}{2017})$
=-1+$\frac{1}{2017}$
=-$\frac{2016}{2017}$.
故选:D.
点评 本题考查了等差数列的通项公式性质及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
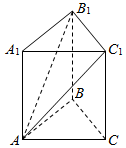 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{6}$,则AA1与平面AB1C1所成的角为( )
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,$A{A_1}=\sqrt{6}$,则AA1与平面AB1C1所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,$\widehat{AB}=\widehat{AF}$,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,$\widehat{AB}=\widehat{AF}$,BF与AD、AO分别交于点E、G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤0} | B. | {x|-1<x<3} | C. | {x|0<x<3} | D. | {x|x≤0或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
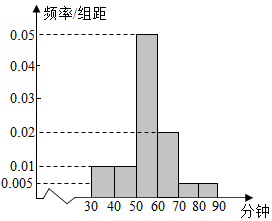 某学校高二年级共有女生300人,现调查她们每天的课外运动时间,发现她们的课外运动时间介于30分钟到90分钟之间,如图是统计结果的频率分布直方图,则她们的平均运动时间大约是56.5分钟.
某学校高二年级共有女生300人,现调查她们每天的课外运动时间,发现她们的课外运动时间介于30分钟到90分钟之间,如图是统计结果的频率分布直方图,则她们的平均运动时间大约是56.5分钟.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com