Question

8．如图所示，BC是半圆O的直径，AD⊥BC，垂足为D，$\widehat{AB}=\widehat{AF}$，BF与AD、AO分别交于点E、G．
（1）证明：∠DAO=∠FBC；
（2）证明：AE=BE．

Answer 1

分析 （Ⅰ）连接FC，OF，利用$\widehat{AB}=\widehat{AF}$，说明OB=OF，然后证明∠AOB=∠FCB，推出∠DAO=∠FBC．
（Ⅱ）证明△OAD≌△OBG，推出OD=OG．然后证明△AGE≌△BDE，即可证明AE=BE．

解答 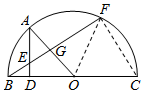证明：（Ⅰ）连接FC，OF，∵$\widehat{AB}=\widehat{AF}$，OB=OF，∴点G是BF的中点，OG⊥BF．
因为BC是⊙O的直径，所以CF⊥BF．∴OG∥CF．∴∠AOB=∠FCB，…（6分）
∴∠DAO=90°-∠AOB，∠FBC=90°-∠FCB，∴∠DAO=∠FBC．…（8分）
（Ⅱ）在Rt△OAD与Rt△OBG中，由（Ⅰ）知∠DAO=∠GBO，
又OA=OB，所以，△OAD≌△OBG，于是OD=OG．
∴AG=OA-OG=OB-OD=BD．…（10分）
在Rt△AGE与Rt△BDE中，由于∠DAO=∠FBC，AG=BD，
所以，△AGE≌△BDE，因此，AE=BE．…（12分）

点评 本题考查三角形的全等的证明，圆周角与几何图形的关系，考查分析问题解决问题的能力．