
分析 设出AB的方程,A,B的坐标,进而把直线与抛物线方程联立消去y,根据韦达定理求得x1+x2和x1x2的表达式,进而利用抛物线方程求得y1y2=的表达式,进而根据AO⊥BO推断出x1x2+y1y2=0,求得b,设△AOB的重心为G(x,y),则x和y的表达式可得,联立后消去k则x和y的关系式可得.
解答 解:显然直线AB的斜率存在,记为k,AB的方程记为:y=kx+b,(b≠0),A(x1,y1),B(x2,y2),将直线方程代入y=x2得:x2-kx-b=0,则有:
△=k2+4b>0①,x1+x2=k②,x1x2=-b③,又y1=x12,y2=x22
∴y1y2=b2;
∵AO⊥BO,∴x1x2+y1y2=0,
得:-b+b2=0且b≠0,
∴b=1,代入①验证,满足;
故y1+y2=k(x1+x2)+2=k2+2;
设△AOB的重心为G(x,y),
则x=$\frac{{x}_{1}+{x}_{2}}{3}$=$\frac{k}{3}$④,y=$\frac{{y}_{1}+{y}_{2}}{3}$=$\frac{{k}^{2}+2}{3}$⑤,
由④⑤两式消去参数k得:G的轨迹方程为$y=3{x}^{2}+\frac{2}{3}$.
故答案为:$y=3{x}^{2}+\frac{2}{3}$.
点评 本题主要考查了抛物线的简单性质.上述求轨迹的方法称为“参数法”,一般先设法将动点坐标用“参数”表示,再消参数.


科目:高中数学 来源: 题型:选择题
| A. | 0<b<a | B. | 0<a<b | C. | a=b | D. | a≤b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
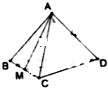 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | -$\frac{π}{3}$ | D. | -$\frac{π}{6}$或$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
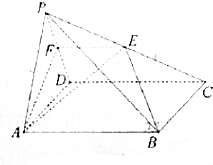 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°,点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$x-y+2=0 | B. | x-$\sqrt{6}$y+1=0 | C. | 4x-y+2=0 | D. | x-4y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,$\frac{π}{2}$),x>sinx | B. | ?x0∈R,sinx0+cosx0=2 | ||
| C. | “?x∈R,3x>0” | D. | ?x0∈R,x0+$\frac{1}{x_0}$=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com