
 .工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算水箱的高为多少时,水箱的容积最大?最大容积是多少?
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
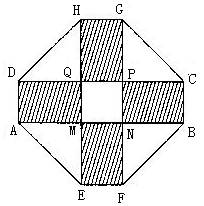
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
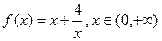 的图像时,.列表如下:
的图像时,.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
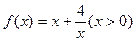 的递减区间是 ,递增区间是 ;
的递减区间是 ,递增区间是 ;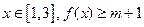 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com