
分析 根据条件作出曲线对应的图象,结合M∩N=∅,转化为直线y=x+b与曲线y=$\sqrt{9-{x}^{2}}$,没有公共点,利用几何法进行求解即可.
解答 解:∵M={(x,y)|y=$\sqrt{9-{x}^{2}}$},N={(x,y)|y=x+b},且M∩N=∅,
∴直线y=x+b与曲线y=$\sqrt{9-{x}^{2}}$,没有公共点,
作出对应的图象如图:当直线y=x+b经过点A(3,0)时,b=y-x=0-3=-3,
当直线y=x+b与上半圆在第二象限相切时,
圆心到直线x-y+b=0的距离d=$\frac{|b|}{\sqrt{2}}$=3,则|b|=3$\sqrt{2}$,
则b=3$\sqrt{2}$或b=-3$\sqrt{2}$,(舍),
则要使M∩N=∅,
则b<-3或b>3$\sqrt{2}$,
即实数b的取值范围是(-∞,-3)∪(3$\sqrt{2}$,+∞),
故答案为:(-∞,-3)∪(3$\sqrt{2}$,+∞)
点评 本题主要考查直线和曲线的位置关系的判断,利用条件转化为几何问题是解决本题的关键.


科目:高中数学 来源: 题型:选择题
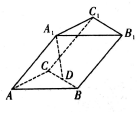 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3.5 | B. | 3.5 | C. | -4.5 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{1}{5}$ | B. | ±$\frac{\sqrt{5}}{5}$ | C. | ±$\frac{2\sqrt{5}}{5}$ | D. | ±$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com