
 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,O为坐标原点,点B在C上,△OBA为等腰直角三角形.分析 (Ⅰ)由题意,有B($\frac{a}{2}$,$\frac{a}{2}$),将点B的坐标代入$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,即可求椭圆C的离心率e;
(Ⅱ)分类讨论,直线方程代入椭圆方程,利用韦达定理,即可求弦|MN|的最大值.
解答 解:(Ⅰ)由题意,有B($\frac{a}{2}$,$\frac{a}{2}$),将点B的坐标代入$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
得a2=3b2,即a2=3(a2-c2),3c2=2a2,
故椭圆C的离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$.…(5分)
(Ⅱ)由题意,得b2=1,a2=3.
当直线l的斜率不存在时,不妨设l的方程为x=1,代入$\frac{{x}^{2}}{3}$+y2=1,
得M(1,$\frac{\sqrt{6}}{3}$),N(1,-$\frac{\sqrt{6}}{3}$),|MN|=$\frac{2\sqrt{6}}{3}$.…(7分)
当直线l的斜率存在时,设l的方程为y=kx+m,由题意,
有$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,即m2=k2+1.
将y=kx+m代入$\frac{{x}^{2}}{3}$+y2=1,得(1+3k2)x2+6kmx+3m2-3=0,
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{-6km}{1+3{k}^{2}}$,x1x2=$\frac{3{m}^{2}-3}{1+3{k}^{2}}$,
所以|MN|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{2\sqrt{6}|k|\sqrt{1+{k}^{2}}}{1+3{k}^{2}}$≤$\frac{2\sqrt{6}|k|\sqrt{1+{k}^{2}}}{2\sqrt{2}|k|\sqrt{1+{k}^{2}}}$=$\sqrt{3}$(当且仅当k2=1时取“=”).
因为$\sqrt{3}$>$\frac{2\sqrt{6}}{3}$,所以|MN|的最大值为$\sqrt{3}$.…(12分)
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
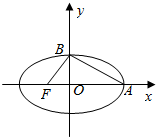 如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.
如图所示,椭圆中心在坐标原点,F为左焦点,当$\overrightarrow{FB}$⊥$\overrightarrow{AB}$时,该椭圆被称为“黄金椭圆”,其离心率为$\frac{\sqrt{5}-1}{2}$,类比“黄金椭圆”,可推算出“黄金双曲线”的离心率e等于$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.
如图,A,B是椭圆W:$\frac{x^2}{3}$+y2=1的两个顶点,过点A的直线与椭圆W交于另一点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
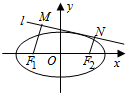 已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.
已知中心在原点,焦点在x轴上的椭圆C过点P(0,$\sqrt{3}$),离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1] | B. | (-$\frac{1}{2}$,1] | C. | (0,$\frac{1}{3}$] | D. | (-$\frac{1}{3}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
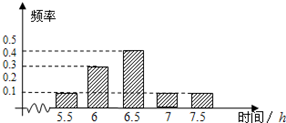 某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.
某机构为了解高三学生的睡眠时间,从该市的所有高三学生中随机抽取了100名,得到他们在某天各自的睡眠时间的数据,结果用下面的条形图表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com