
���� ��1����ֱ��l��y=1����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����У�����Բ��������Ϊ$\frac{\sqrt{2}}{2}$���ɵã�b=1��$\frac{c}{a}=\frac{\sqrt{2}}{2}$��a2=b2+c2��������ü��ɵó���
��2��ֱ�߷�������Բ����������Ϊ$��1+2{k}^{2}��{x}^{2}+4\sqrt{2}kx$+2=0����P��x1��y1����Q��x2��y2��������0�����ø���ϵ���Ĺ�ϵ�ɵã�y1y2=k2x1x2+$\sqrt{2}k$��x1+x2��+2.$\overrightarrow{OP}•\overrightarrow{OQ}$=x1x2+y1y2=$\frac{2}{3}$�����k2=1������|PQ|=$\sqrt{��1+{k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$�����ɵó�S��MPQ��
��� �⣺��1����ֱ��l��y=1����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�����У�����Բ��������Ϊ$\frac{\sqrt{2}}{2}$��
��b=1��$\frac{c}{a}=\frac{\sqrt{2}}{2}$��a2=b2+c2��
�������b=c=1��a2=2��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}$=1��
��2������$\left\{\begin{array}{l}{y=kx+\sqrt{2}}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$����Ϊ$��1+2{k}^{2}��{x}^{2}+4\sqrt{2}kx$+2=0��
��P��x1��y1����Q��x2��y2������=32k2-8��1+2k2����0�����k2$��\frac{1}{2}$��
��x1+x2=$\frac{-4\sqrt{2}k}{1+2{k}^{2}}$��x1x2=$\frac{2}{1+2{k}^{2}}$��
��y1y2=$��k{x}_{1}+\sqrt{2}����k{x}_{2}+\sqrt{2}��$=k2x1x2+$\sqrt{2}k$��x1+x2��+2=$\frac{2{k}^{2}}{1+2{k}^{2}}$-$\frac{8{k}^{2}}{1+2{k}^{2}}$+2=$\frac{2-2{k}^{2}}{1+2{k}^{2}}$��
��$\overrightarrow{OP}•\overrightarrow{OQ}$=x1x2+y1y2=$\frac{2}{1+2{k}^{2}}$+$\frac{2-2{k}^{2}}{1+2{k}^{2}}$=$\frac{4-2{k}^{2}}{1+2{k}^{2}}$=$\frac{2}{3}$�����k2=1$��\frac{1}{2}$��
��|PQ|=$\sqrt{��1+{k}^{2}��[��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2����\frac{32}{9}-\frac{8}{3}��}$=$\frac{4}{3}$��
��M������l��y=x+$\sqrt{2}$��
��$\frac{|m+\sqrt{2}|}{\sqrt{2}}$=1��m��0�����m=-2$\sqrt{2}$��
��S��MPQ=$\frac{1}{2}��1��\frac{4}{3}$=$\frac{2}{3}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ���ҳ���ʽ�������������������ʡ�������������㹫ʽ����������������������������������⣮


 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
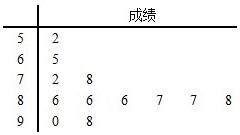 Ϊ��ʵ����Ժ��ʮ���塱�滮�е�����������裬ijҽԺ��������������˵����ʽ���������Ӹ�����ȫ���������У������ȡ12���������ʽ������ԣ����Գɼ����ٷ��ƣ��Ծ�Ҷͼ��ʽ��ͼ���������������ʽ��������ɼ�������80��Ϊ������
Ϊ��ʵ����Ժ��ʮ���塱�滮�е�����������裬ijҽԺ��������������˵����ʽ���������Ӹ�����ȫ���������У������ȡ12���������ʽ������ԣ����Գɼ����ٷ��ƣ��Ծ�Ҷͼ��ʽ��ͼ���������������ʽ��������ɼ�������80��Ϊ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��1�� | B�� | ��-1��-1�� | C�� | ��1��-1�� | D�� | ��-1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��b��a | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{1}{7}$��+�ޣ� | B�� | [$\frac{1}{7}$��$\frac{1}{3}$�� | C�� | ��-�ޣ�$\frac{1}{3}$�� | D�� | ��-�ޣ�$\frac{1}{7}$]�ȣ�$\frac{1}{3}$��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com