
分析 (1)将已知等式两边平方,利用同角三角函数基本关系式即可得解.
(2)利用同角三角函数基本关系式及立方差公式即可得解.
(3)把sin4θ+cos4θ转化为含有sinθ•cosθ的代数式得答案;
解答 解:(1)∵sinθ-cosθ=$\frac{1}{2}$,
∴两边平方可得:1-2sinθcosθ=$\frac{1}{4}$,解得:sinθcosθ=$\frac{3}{8}$.
(2)sin3θ-cos3θ=(sinθ-cosθ)(sin2θ+sinθcosθ+cos2θ)=$\frac{1}{2}$×(1+$\frac{3}{8}$)=$\frac{11}{16}$.
(3)sin4θ+cos4θ=(sin2θ+cos2θ)2-2sin2θcos2θ=1-2×($\frac{3}{8}$)2=$\frac{23}{32}$.
点评 此题考查了同角三角函数基本关系的运用,考查了计算能力和转化思想,熟练掌握基本关系是解本题的关键,属于基础题.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $({-1,\frac{3}{2}})$ | B. | $({-∞,-1})∪({\frac{3}{2},+∞})$ | C. | $({1,\frac{3}{2}})$ | D. | $({-∞,1})∪({\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2) | B. | (2,2)或(-2,-2) | C. | (-2,-2) | D. | (2,2)或(2,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{{2}^{2016}}$ | B. | 2016×22015 | C. | 2016×22016 | D. | $\frac{2016}{{2}^{2015}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
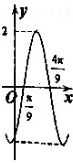
| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | B. | $φ=\frac{π}{9}$ | ||
| C. | 函数f(x)在区间$[0,\frac{π}{4}]$上是增函数 | D. | 函数f(x)的图象关于直线$x=\frac{5π}{6}$对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com