
分析 (Ⅰ)由条件利用余弦定理,解方程组求得cosC的值.
(Ⅱ)利用同角三角函数的基本关系求得sinC的值,利用二倍角公式、两角和差的三角公式求得cos(2C+$\frac{π}{3}$)的值.
解答 解:(Ⅰ)△ABC中,∵cosB=$\frac{1}{3}$,ac=6,b=3,a>c,
∴由余弦定理得,9=a2+c2-2•6•$\frac{1}{3}$,解得 $\left\{\begin{array}{l}{a=3}\\{c=2}\end{array}\right.$,
∴cosC=$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{7}{9}$.
(Ⅱ)由(Ⅰ)利用同角三角函数的基本关系可得sinC=$\sqrt{{1-cos}^{2}C}$=$\frac{4\sqrt{2}}{9}$,
∴sin2C=2sinCcosC=2•$\frac{4\sqrt{2}}{9}$•$\frac{7}{9}$=$\frac{56\sqrt{2}}{81}$.
∴cos2C=2cos2C-1=$\frac{17}{81}$.
∴cos(2C+$\frac{π}{3}$)=cos2Ccos$\frac{π}{3}$-sin2Csin$\frac{π}{3}$=$\frac{17-56\sqrt{6}}{162}$.
点评 本题主要考查同角三角函数的基本关系、二倍角公式、两角和差的三角公式的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
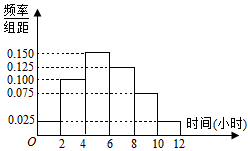 为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
为调查某乡镇中心小学的学生每周平均体育运动时间的情况,收集了20位学生每周平均体育运动时间的样本数据(单位:小时).这20位学生每周平均体育运动时间的频率分布直方图如图所示,其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,+∞) | B. | (-∞,$\frac{1}{3}$) | C. | (-3,$\frac{1}{3}$) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | 30 | C. | 28 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com