
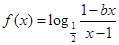 为奇函数,
为奇函数,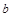 为常数.
为常数.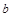 的值;
的值; 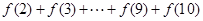 的值;
的值;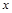 的值,不等式
的值,不等式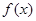 >
>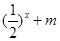 恒成立,求实数
恒成立,求实数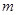 的取值范围.
的取值范围.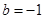 ;
;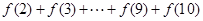 =
=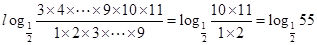 ;
;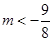 。
。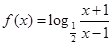 ,得
,得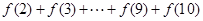 =
=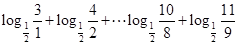 这是求解此步的关键,然后再利用对数的运算法则求值即可。
这是求解此步的关键,然后再利用对数的运算法则求值即可。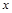 的值,不等式
的值,不等式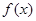 >
>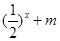 恒成立转化为当
恒成立转化为当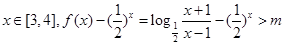 恒成立,然后再构造函数:
恒成立,然后再构造函数: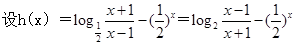 研究出h(x)是增函数,从而可求出h(x)的最小值,问题得解。
研究出h(x)是增函数,从而可求出h(x)的最小值,问题得解。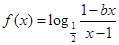 为奇函数
为奇函数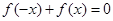 ,即
,即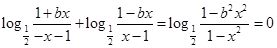 …2分
…2分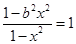 ,解得
,解得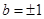 ………………………4分
………………………4分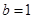 显然不成立,舍去。所以
显然不成立,舍去。所以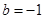 ………………………………………5分
………………………………………5分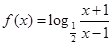
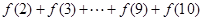 =
=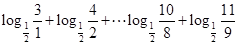 ……6分
……6分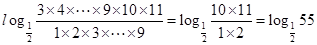 ………………………9分
………………………9分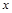 的值,不等式
的值,不等式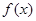 >
>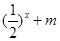 恒成立
恒成立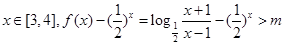 恒成立…………………10分
恒成立…………………10分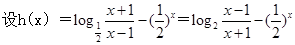 …………………11分
…………………11分 在[3,4]上单调递增,
在[3,4]上单调递增,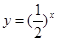 单调递减
单调递减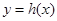 在[3,4]上单调递增 …………………………………………12分
在[3,4]上单调递增 …………………………………………12分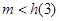 即可
即可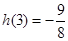 所以
所以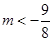 ……………………………………………14分
……………………………………………14分


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com