Question

5．假设在10秒内的任何时刻，两条不相关的短信机会均等第进入同一部手机，若这两条短信进入手机的时间之差大于3秒，手机就会不受到干扰，则手机不受到干扰的概率为$\frac{49}{100}$．

Answer 1

分析 根据几何概型的概率公式求出对应的测度，即可得到结论

解答 解：分别设两个互相独立的短信收到的时间为x，y．则所有事件集可表示为0≤x≤10，0≤y≤10．
由题目得，如果手机受则到干扰的事件发生，必有|x-y|≤3．
则该事件即为x-y=3和y-x=3在0≤x≤10，0≤y≤10的正方形中围起来的图形，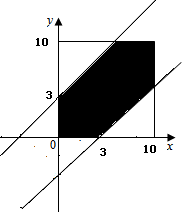
即图中阴影区域，而所有事件的集合即为正方型面积10²=100，
阴影部分的面积2×$\frac{1}{2}$（10-3）²=49，
所以阴影区域面积和正方形面积比值即为手机不受到干扰的概率为$\frac{49}{100}$．
故答案为：$\frac{49}{100}$

点评 本题主要考查几何概型的概率的计算，分别求出对应区域的面积是解决本题的关键，比较基础．