Question

18．已知平面上的曲线l及点P，在l上任取一点Q，线段PQ长度的最小值称为点P到曲线l的距离，记作d（P，l）．
（1）求点P（3，4）到曲线l：x²+y²=4的距离d（P，l）；
（2）设曲线l：$\left\{\begin{array}{l}{{y}^{2}=1（-1＜x＜1）}\\{（x-1）^{2}+{y}^{2}=1（1≤x≤2）}\\{（x+1）^{2}+{y}^{2}=1（-2≤x≤-1）}\end{array}\right.$，求点集S={P|2＜d（P，l）≤3}所表示图形的面积；
（3）设曲线l₁：y=0（-1≤x≤1），曲线l₂：x²+y²=1，求出到两条曲线l₁，l₂距离相等的点的集合Ω={P|d（P，l₁）=d（P，l₂）}．

Answer 1

分析 （1）由题意可得|OP|=5，由圆的几何性质可得d（P，l）=|OP|-2=3；
（2）画出点集S={P|2＜d（P，l）≤3}所表示图形，分|x|≤1的部分与|x|＞1的部分求出图形面积，作和得答案；
（3）画出集合Ω={P|d（P，l₁）=d（P，l₂）}的图象分点在圆x²+y²=1上，点在圆x²+y²=1外及点在圆x²+y²=1内的情况，分类求解得答案．

解答 解：（1）由题意可得|OP|=5，由圆的几何性质可得d（P，l）=|OP|-2=3；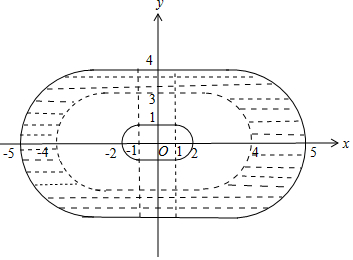
（2）点集S={P|2＜d（P，l）≤3}所表示图形如阴影部分所示：
在|x|≤1的部分，图形为上下两个长为2，宽为1的长方形，面积为2×2×1=4．
在|x|＞1的部分，图形为左右两个半圆，面积为π×（5-1）²-π×（4-1）²=7π．
综上所述，点集S={P|2＜d（P，l）≤3}所表示图形的面积为4+7π；
（3）集合Ω={P|d（P，l₁）=d（P，l₂）}的图象如图所示：
a、考虑点在圆x²+y²=1上的情况，显然点A（-1，0）与点B（1，0）在集合Ω中．
b、考虑点在圆x²+y²=1外的情况，显然点A（-1，0）左侧的点{（x，y）|y=0，x＜-1}与点B（1，0）右侧的点{（x，y）|y=0，x＞1}在集合Ω中．
c、考虑点在圆x²+y²=1内的情况，显然圆心O（0，0）不在集合Ω中．
设点P（x，y）为圆内异于圆心的任意一点，过点P作PC⊥x轴与点C，连接OP并延长与曲线l₂交于点Q，
则有点C（x，0），Q（$\frac{x}{\sqrt{{x}^{2}+{y}^{2}}}$，$\frac{y}{\sqrt{{x}^{2}+{y}^{2}}}$），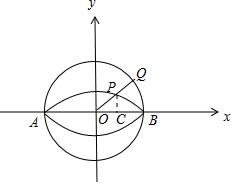
若|PC|=|PQ|，则|y|=$\sqrt{（x-\frac{x}{\sqrt{{x}^{2}+{y}^{2}}}）^{2}+（y-\frac{y}{\sqrt{{x}^{2}+{y}^{2}}}）^{2}}$，
即|y|=$\sqrt{（{x}^{2}+{y}^{2}）（1-\frac{1}{\sqrt{{x}^{2}+{y}^{2}}}）^{2}}=\sqrt{（\sqrt{{x}^{2}+{y}^{2}}-1）^{2}}$．
即${y}^{2}=（\sqrt{{x}^{2}+{y}^{2}}-1）^{2}={x}^{2}+{y}^{2}-2\sqrt{{x}^{2}+{y}^{2}}+1$，即$2\sqrt{{x}^{2}+{y}^{2}}={x}^{2}+1$．
即4（x²+y²）=（x²+1）²，
∴$y=±\frac{1}{2}（1-{x}^{2}）$（-1＜x＜1）．
综上所述，Ω={（x，y）|y=0，|x|≥1}∪{（x，y）|y=$±\frac{1}{2}（1-{x}^{2}）$，-1＜x＜1}．

点评 本题考查曲线与方程，考查数形结合的解题思想方法，关键是对题意的理解，是中档题．